STA:一文讀懂StarkNet零知識遞歸證明：STARK_starl幣有投資價值嗎

StarkNet零知識遞歸證明—STARK已上線，遞歸在成本和延遲方面的優勢異常顯著，還會催生L3和應用遞歸等新機會。

原文：《RecursiveSTARKs》byStarkWare核心工程師GidiKaempfer

翻譯：「StarkNet中文」社區

作者：技術最前沿

概要

遞歸證明上線主網，用一個證明來擴展StarkEx應用程序和StarkNet

遞歸證明提升擴展性，降低成本和延遲

遞歸證明為L3和其他妙用創造了條件

來看看遞歸證明的博文吧，超酷的

倍數擴展！

由Cairo通用計算提供支持的遞歸證明現已投入生產。這標志著STARK對L2擴展能力的重大提升。單一證明寫入以太坊的交易數量可快速成倍增加。

迄今為止，STARK證明通過將數萬甚至數十萬個交易「匯總」成單一證明寫入以太坊來實現擴展。通過遞歸，許多這樣的證明可以「匯總」成一個單一證明。

這種方法現已應用于眾多基于Cairo的應用程序：在StarkWare的SaaS擴展引擎StarkEx和無需許可的RollupStarkNet上運行的應用程序。

迄今發展歷程

自2020年3月主網上線首個證明產生以來，STARK證明至今經歷了不同發展階段。

Binance礦池將暫停發放DASH挖礦收益:5月22日消息，據官方公告，由于Dash Corev19激活期間的最新情況，Dash（DASH）網絡暫停了新區塊的更新。因此，Binance礦池將暫停發放DASH挖礦收益直至DASH區塊恢復，不再另行通知。[2023/5/22 15:18:55]

STARK擴展

2020年6月，第一個STARK擴展解決方案StarkEx在以太坊主網部署。StarkEx有一個證明器可以在鏈下執行大型計算，生成一個STARK證明表示交易準確性，還有一個驗證器在鏈上驗證證明的準確性。第一次部署由StarkWare工程師從零開始親自操刀，因此StarkEx的功能極大受限。最終我們決定，需要一種支持證明通用計算的編程語言。這樣，Cairo便應運而生。

Cairo編程語言

2020年夏天，Cairo首次亮相以太坊主網。Cairo即CPU代數中間代碼(CPUAlgebraicIntermediateRepresentation)，內含一個用于驗證相應「CPU」指令集的單一AIR。Cairo為更復雜的業務邏輯、任意可計算命題(computationalstatements)打開了編碼證明的大門，而且更快、更安全。一個Cairo程序可以證明相應應用程序的執行邏輯。但一個Cairo程序也可以集合多個此類應用程序，這就是SHARP。

SHARP

SHARP即共享證明器(SHARedProSver)，可以聚合幾個獨立應用程序的交易，并在一個單一的STARK證明中證明。應用程序可以組合不同批量交易，更快填滿STARK證明的容量。交易處理速度和延遲都有所提高。遞歸證明是下一代前沿技術，不僅適用于一些硬編碼邏輯，而且適用于通用計算。

分析師：比特幣可能在2023年反彈至50,000美元:金色財經報道，根據受歡迎的市場分析師 Mags 強調的歷史價格分形，比特幣可能在 2023 年反彈至 50,000 美元。BTC 的價格在 2023 年 3 月突破了 16,000-25,000 美元區間，促使 Mags 強調其與 2015 年 10 月突破 200-300 美元區間的相似之處。由于這導致比特幣在 2016 年 6 月上漲至 700 美元，分析師認為這種情況可能會在 2023 年重演，BTC 價格將翻一番至 50,000 美元。[2023/4/8 13:51:15]

要了解遞歸證明的全部優勢，有必要進一步了解SHARP迄今為止是如何執行證明的。圖1描繪了一個典型的非遞歸流程：

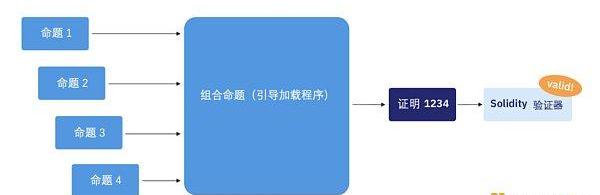
圖1：典型非遞歸證明流程

在這個流程中，命題逐漸到達。容量達到一定閾值時，會生成一個大型組合命題(Train)。只有在收到所有單獨命題后，才能證明此組合命題。此證明需要很長時間。

證明極其龐大的命題最終會受到內存等可用計算資源的限制。在遞歸之前，這實際上是限制STARK證明可擴展性的一大障礙。

什么是遞歸證明？

通過STARK證明，證實命題所花費的時間與執行命題所花費的時間大致呈線性關系。此外，如果證明一個命題需要的時間為T，那么驗證證明所需要的時間大約為log(T)，這通常被稱為「對數壓縮」。換句話說，使用STARK讓用戶在驗證命題上的時間要比計算命題的時間少得多。

2023年迄今灰度GBTC和ETHE表現超越現貨比特幣和以太坊:金色財經報道，2023年迄今灰度的比特幣信托基金GBTC和以太坊信托基金ETHE表現超越了現貨比特幣（BTC）和以太坊（ETH）。數據顯示，GBTC今年上漲95%，折價收窄至約40%（2023年1月曾一度低至50%）；ETHE今年上漲83%，折價收窄至約51%（2023年1月曾一度低至60%），相比之下比特幣同期漲幅為72%，以太坊上漲60%。需要注意的是，隨著以太坊上海升級的臨近，下周市場可能會出現波動。[2023/4/6 13:47:54]

Cairo允許表達通用計算命題，這些命題可以經STARK證明所證實，再經相應的STARK驗證器驗證。

這就是執行遞歸的機會所在：就像可以寫一個Cairo程序來證明成千上萬的交易正確性，也可以寫一個Cairo程序來驗證多個

STARK證明。可以生成一個證明來驗證多個「上游」證明的有效性。這就是我們所說的遞歸證明。

由于對數壓縮和證明時間大致呈線性關系，證實STARK證明所需的時間相對較短。

在實現遞歸時，SHARP可以一收到命題就可以對其進行驗證。證明可以各種模式反復地合并成遞歸證明，直到在某個點上，產生的證明提交給鏈上驗證者合約。圖2就是典型的遞歸證明模式：

Alchemix Finance DAO批準ALCX代幣回購計劃相關提案:2月7日消息，加密借貸協議Alchemix Finance背后的DAO周一批準一項提案，將支持其Treasury和Yield Farming活動的部分現金轉移到其原生ALCX代幣回購計劃中。

該提案旨在通過指示Alchemix將其Yield Farming收入的三分之一用于購買ALCX代幣來支持alAssets。新模式應該產生足夠的收入來“支付所有費用，并讓Treasury有適度的盈余”。Alchemix Finance Treasury目前擁有100萬美元的穩定幣和200萬美元的以太坊，每年消耗高達120萬美元。

提案稱，“它將我們最大的開支變成了該協議的主要收入來源。”（CoinDesk）[2023/2/7 11:52:01]

圖2：典型遞歸證明流程

在本例中，有四個命題發送給SHARP。這些命題各自平行證明。然后，每一對證明都由一個遞歸驗證器命題來驗證，由此產生一個證明。這一命題證實有兩個證明經過驗證。接下來，通過遞歸驗證器命題再次合并這兩個證明。這就產生了一個證明，證實所有四個原始命題。此證明最終可以提交到鏈上，由Solidity驗證器智能合約進行驗證。

遞歸證明的直接優勢

降低鏈上成本

毫無疑問，我們實現了將多個證明「壓縮」成一個，這意味著每筆交易鏈上驗證成本會大幅更低。

使用遞歸證明可以消除至今限制證明大小的計算資源障礙，因為每個命題容量有限，都可以單獨證明。因此當使用遞歸時，遞歸的有效組合命題(Train)的容量幾乎是無限，每筆交易成本可以降低好幾個數量級。

Mellow Protocol完成275萬美元種子輪融資，Robot Ventures、Arrington Capital、ParaFi領投:8月26日消息，Uniswap V3 LP自動化協議Mellow Protocol宣布完成275萬美元種子輪融資，Robot Ventures、Arrington Capital、ParaFi領投，其他投資者包括P2P Capital、Lemniscap、Focus Labs、Principle Ventures、Primitive Ventures、NEMO Ventures等。[2022/8/26 12:49:06]

在實際操作中，降低成本取決于可接受的延遲。此外，由于每個證明通常也伴隨相應鏈上數據輸出，因此與單個證明一起寫入鏈上的數據量也會有限。盡管如此，將成本降低一個數量級，甚至繼續提升性能都可以輕松實現。

降低延遲

遞歸證明模式可降低證明大型組合命題延遲。有兩個因素起到作用：

1.接收的命題可以并行證明。

2.無需等到Train中的最后一個命題到達即可證明。相反，有新命題加入可以隨時與證明結合。也就是說，加入Train的最后一個命題的延遲，大致上是證明最后一條命題所需的時間加上證明遞歸驗證器命題所需的時間。

我們正在積極開發和優化證明遞歸驗證器命題的延遲問題。預計幾個月內證明遞歸驗證器命題會達到幾分鐘的數量級。因此，一個高效的SHARP延遲可控制在幾分鐘到幾小時，延遲長短取決于對每筆交易鏈上成本的取舍。這是對SHARP延遲的重大改進。

促進L3應用

用Cairo開發的遞歸驗證器命題也開啟了向StarkNet提交證明的可能性，因為該命題可以寫入StarkNet智能合約。這允許在StarkNetL2公共網絡上部署L3。

遞歸模式也適用于來自L3的聚合證明，由L2上的單個證明驗證。因此，L3也可以實現超大規模擴展。

更多妙用

應用遞歸

遞歸為希望進一步擴展其成本和性能的平臺和應用程序開辟了更多機會。

每個STARK證明證實應用于某些「公開輸入」的命題有效性。從概念上來說，STARK遞歸將具有兩個輸入的兩個證明壓縮為一個具有兩個輸入的證明。換句話說，雖然證明的數量減少，但輸入數量未變。然后，輸入通常由應用程序用以更新L1上的某些狀態。

如果遞歸命題可以在應用層感知，即識別應用程序本身的語義，那么遞歸命題既可以將兩個證明壓縮為一個，也可以將兩個輸入組合為一個。最終的命題證實基于應用程序語義的輸入組合的有效性，這就是應用遞歸。

圖3：應用遞歸示例

命題1證明從A到B的狀態更新，而命題2驗證從B到C的進一步更新。命題1和命題2的證明可以合并為第三個命題，直接證明從A到C的更新。通過應用類似的遞歸邏輯，可以非常顯著地降低狀態更新的成本，達到最終延遲要求。

應用遞歸的另一個重要示例是壓縮來自多個證明的匯總數據。例如，對于像StarkNet這樣的有效性證明Rollup，L2每次存儲更新也作為傳輸數據在L1更新，確保數據可用性。但是，不需要為同一個存儲單元發送多次更新，因為只有經過證明驗證過的交易最終才能滿足數據可用性。此優化已在單個StarkNet區塊中執行。但是，通過為每個區塊生成證明，應用遞歸可以壓縮多個L2區塊匯總數據。這可以顯著降低成本，降低L2出塊時間，而不會犧牲L1更新的可擴展性。

值得注意的是：應用遞歸可以與前面描述的應用通用遞歸結合使用。但這兩種優化互無關聯。

降低鏈上驗證器的復雜性

STARK驗證器的復雜性取決于用以驗證的命題類型。特別是對于Cairo命題，驗證器的復雜性取決于Cairo語言中允許的特定要素，更具體地說，是支持的內置項。

Cairo語言不斷發展并提供越來越多有用的內置項。另一方面，遞歸驗證器只需要使用一小部分內置項。因此，遞歸SHARP可以通過支持遞歸驗證器中的完整語言來成功支持Cairo中的任何命題。具體來說，L1上的Solidity驗證器只需要驗證遞歸證明，因此驗證器可以僅限于驗證Cairo語言一個更穩定的子集：L1驗證器不需要隨最新、最穩定的內置項更新。換句話說，命題不斷演化，復雜的驗證就交由L2處理，L1驗證器只需要驗證簡單、穩定的命題。

減少計算足跡

在遞歸之前，聚合多個命題為一個證明受到可用計算實例上可以證明的命題大小的限制。

有了遞歸，無需再證明如此龐大的命題。因為有了更多又小又便宜的計算實例可供使用。這使得在更多的物理和虛擬環境中部署證明器實例成為可能。

總結

通用計算的遞歸證明現已為包括StarkNet在內以太坊主網上的多個產品系統服務。

由于可以不斷改進，遞歸的優勢會逐步顯現。并行計算的潛力得以發揮后，Gas費降低，延遲改善，超高擴展性終將實現。

遞歸在成本和延遲方面的優勢異常顯著，還會催生L3和應用遞歸等新機會。遞歸驗證器持續優化，性能和成本效益也都會逐漸提升。

附錄

原文：RecursiveSTARKs

https://medium.com/starkware/recursive-starks-78f8dd401025

原文：Youtube:StarkEx-HowDoesitWork?

https://www.youtube.com/watch?v=P-qoPVoneQA

原文：Hello,Cario!

https://medium.com/starkware/hello-cairo-3cb43b13b209

原文：Hello,Cario!

https://starkware.co/cairo/

原文：WikipediaEntry:Recursion

https://en.wikipedia.org/wiki/Recursion

原文：《分形式擴容：從L2到L3》

https://mirror.xyz/starknet-zh.eth/-5oiKxwShIOzGUwuQJzIl070wopcPjqBcypVjRvyC1E

Tags：STAARKSTARSTARKpSTAKE Staked BNBMARKETINGstarl幣有投資價值嗎StarkNet

OKB