SCR:Scroll聯合創始人：如何從0到1構建zkEVM_CRO

演講分成四個部分，第一部分張燁介紹了開發背景以及我們為什么首先需要zkEVM以及為什么它在最近兩年間變得如此受歡迎，第二部分通過一個完整的流程，講解如何從頭開始構建zkEVM包括算術化和證明系統，第三部分通過一些有趣的研究問題來談論了Scroll在構建zkEVM時遇到的問題，最后介紹了一些其他使用zkEVM的應用。

背景和動機

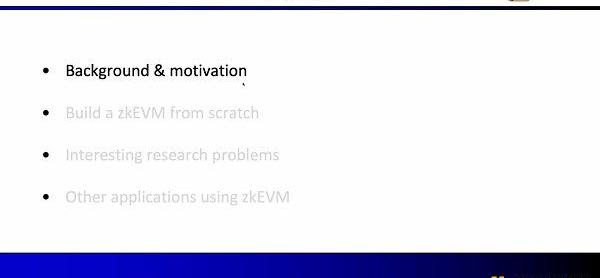
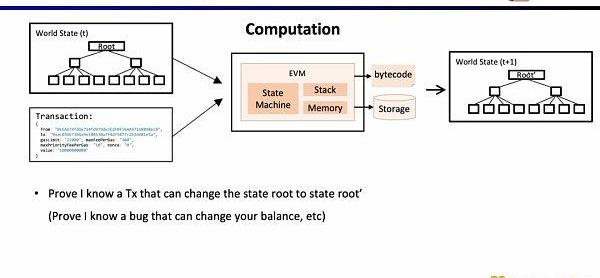
傳統的Layer1區塊鏈會有一些節點通過P2P網絡共同維護。他們在收到用戶的交易時，會在EVM的虛擬機內執行，讀取調用合約和存儲，并依照交易更新全局的狀態樹。

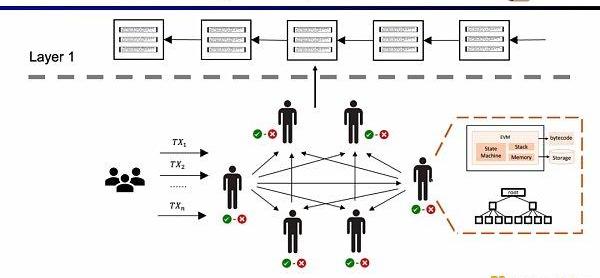
這樣的架構的優勢在于去中心化和安全性，缺陷就是在L1上的交易手續費昂貴，并且交易確認緩慢。

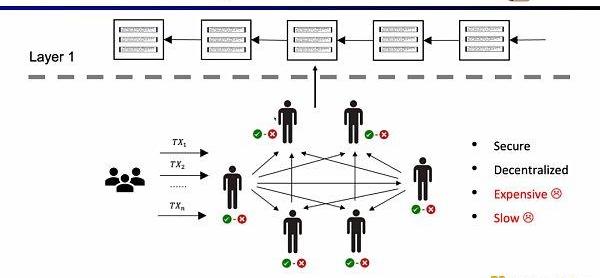
ZK-Rollup的架構中，L2網絡只需將數據和驗證數據正確性的證明上傳至L1，其中證明通過零知識證明電路計算而來。

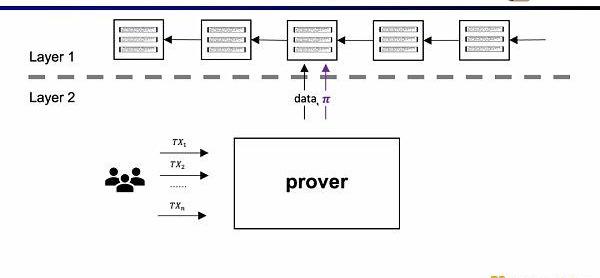
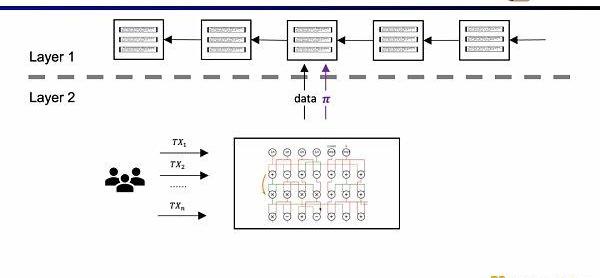
在早期的ZK-Rollup中，電路是針對特定應用而設計，用戶需要將交易發送給不同的證明者，然后不同應用的ZK-Rollup再將自己的數據和證明提交至L1。這樣帶來的問題是，喪失了原先L1合約的可組合性。

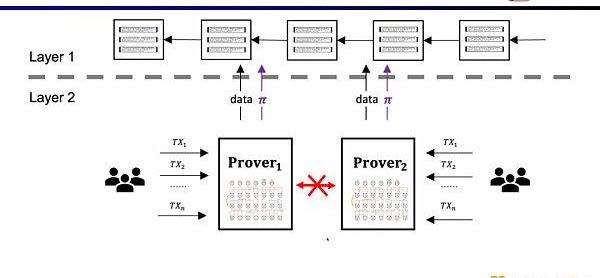
Scroll所要做的是原生的zkEVM方案，是一種通用型的ZK-Rollup。這樣不僅對用戶而言更友好，對于開發者而言也可以獲得在L1上的開發體驗。當然這背后的開發難度非常之大，并且現在的證明生成的代價也非常高。

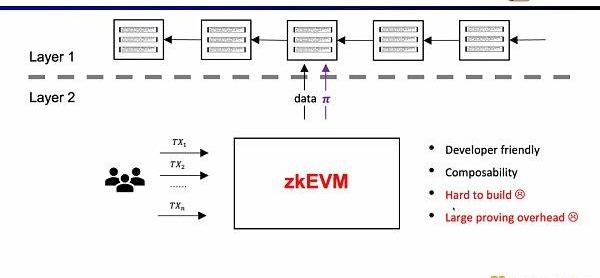
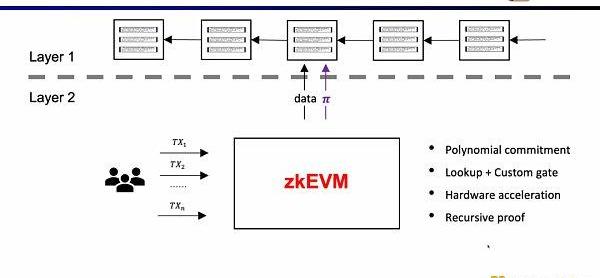
幸運的是，零知識證明的效率在過去兩年里已經大幅提高了，這也是為什么在最近兩年zkEVM變得如此受歡迎。至少有四個原因讓它變得可行，第一是多項式承諾的出現，在原先Groth16證明系統下，約束的規模非常之龐大，而多項式承諾可以支持更高階的約束，縮小證明規模；第二是查找表和自定義門的出現，可以支持更靈活的設計，使證明更加高效；第三是硬件加速方面的突破，通過GPU，FPGA和ASIC可以將證明時間縮短1-2個數量級，第四是在遞歸證明下，可以將多個證明壓縮成一個證明，使得證明變得更小更易于驗證。所以結合這四個因素，零知識證明的生成效率要比兩年前高出三個數量級，這也是Scoll的起源。

LayerZero宣布新增支持Scroll測試網:6月14日消息，跨鏈互操作性協議LayerZero在推特上宣布已在Scroll測試網上線，并在文檔中列出endpoint信息。

此前6月8日消息，LayerZero發推稱已新增支持Arbitrum Nova。[2023/6/15 21:37:24]

根據JustinDrake的定義，zkEVM可以分為三類，第一類是語言級別的兼容，主要原因是EVM不是為ZK而設計，有很多對ZK不友好的操作碼，因此會造成大量的額外開銷。因此像Starkware和zkSync選擇在語言層面將Solidity或者Yul編譯到ZK友好的編譯器中。

第二類是Scroll在做的字節碼層面的兼容，是直接證明EVM的字節碼處理正確與否，直接繼承了以太坊的執行環境。在這里可做的一些取舍是，使用和EVM不一樣的狀態根，例如使用ZK友好的數據結構。Hermez和Consensys也在做類似的事情。

第三類是共識層面的兼容，這里的取舍在于不僅需要保持EVM不變，還包括儲存結構等實現以太坊完全兼容，代價是需要更長的證明時間。而Scroll正在和以太坊基金會的PSE團隊合作構建，來實現以太坊的ZK化

從0到1構建zkEVM

第二部分，張燁向大家展示了如何從零開始建立ZKVM。

完整流程

首先，在ZKP的前端部分，你需要通過數學的算術化來表示你的計算，最常用的就是線性的R1CS，以及Plonkish和AIR。通過算術化得到約束后，在ZKP的后端你需要運行證明算法，來證明計算正確性，這里列舉了最常用的多項式交互式諭示證明(PolynomialIOP)和多項式承諾方案(PCS)。

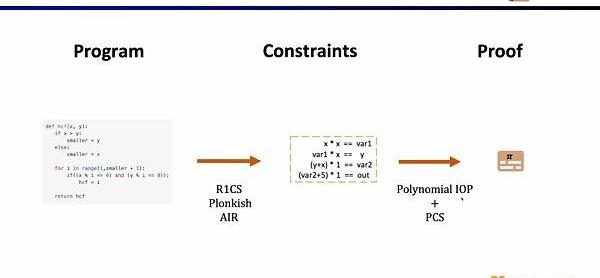
在這里我們需要證明zkEVM，Scroll使用的是Plonkish，PlonkIOP，以及KZG的組合。

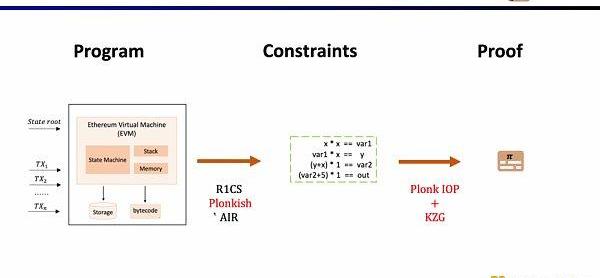
為了理解我們為什么使用這三者的方案。我們首先從最簡單的R1CS開始，R1CS中的約束，是線性組合乘以線性組合等于線性結合。你可以加上任何變量的線性組合而沒有額外的開銷，但是在每個約束中階數最大是2。因此對于階數較高的運算，需要的約束就越多。

Scroll在Goerli測試網推出以太坊L2網絡zk-EVM的測試網版本:金色財經報道，Scroll在Goerli測試網上發布了其以太坊L2網絡的測試網版本，這是將zk-EVM從pre-alpha轉移到alpha的測試階段。到目前為止，Scroll可以在基于該項目的以太坊克隆的測試網上進行試用。測試網的代碼將是開源的，這意味著該網絡可以開始建立彈性。此外，Goerli測試網和Scroll之間已經建立了一個橋梁來轉移資產。

據悉，Zk-EVM是建立在以太坊上的第2層網絡，它使用零知識證明來實現可擴展性。[2023/2/28 12:32:53]

而在Plonkish中，你需要將所有的變量填入表格，包括輸入，輸出以及中間變量的見證。在此之上，你可以定義不同的約束。在Plonkish中有三種類型的約束可以使用。

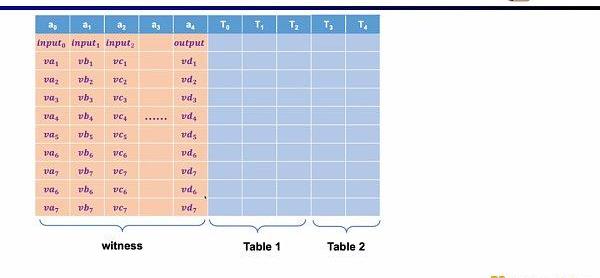
第一種約束是自定義門，你可以定義不同單元格之間的多項式約束關系，例如va3*vb3*vc3-vb4=0。相比R1CS來說，階數可以更高，因為你可以定義任何一個變量的約束，并且可以定義一些非常不一樣的約束。

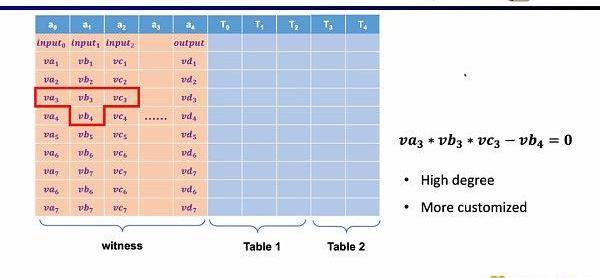
第二種約束是Permuation，即等價性校驗(equalitychecks)。可以用來檢查不同單元格的等價性，常用于關聯電路中的不同門，比如證明上一個門的輸出等于下一個門的輸入。

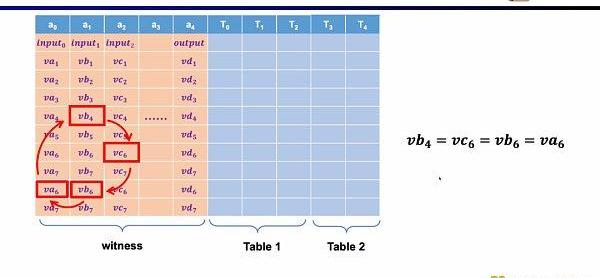
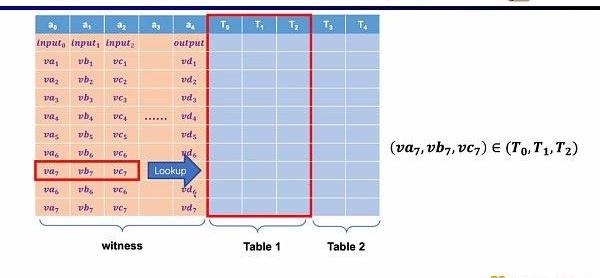
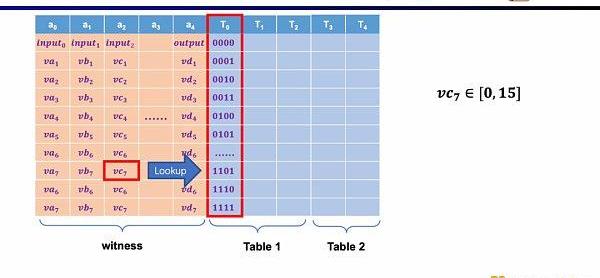
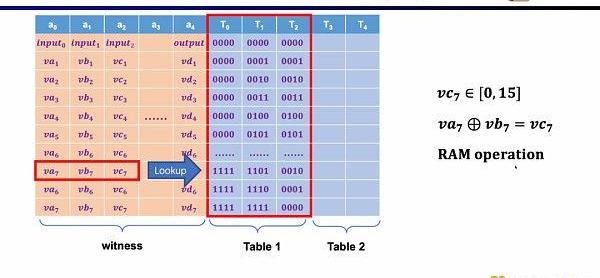
最后一種約束是查找表(LookupTable)。我們可以將查找表理解成變量之間存在一個關系，該關系可以表示成一個表。例如我們想要證明vc7在0-15范圍內，在R1CS中你首先需要把這個數值分解為4位二進制，然后證明每位在0-1的范圍內，這將需要四個約束。而在Plonkish中，你可以將所有可能的范圍列在同一列，只需要證明vc7屬于該列即可，這對范圍證明非常高效，在zkEVM中，查找表對于證明內存讀寫非常有用。

Web3隱私初創公司Sunscreen完成465萬美元種子輪融資:7月18日消息，Web3隱私初創公司Sunscreen宣布完成465萬美元種子輪融資，Polychain Capital領投，Northzone、Coinbase Ventures、dao5和Naval Ravikan、以及Entropy創始人Tux Pacific等天使投資人參投。該公司目前已開發出了一個編譯器，讓工程師更容易構建FHE程序，同時還宣布啟動一項贈款計劃以資助使用FHE的開發人員、學者和研究人員。（TechCrunch）[2022/7/19 2:21:42]

小結一下，Plonkish同時支持自定義門，等價性校驗和查找表，可以非常靈活的滿足不同的電路需要。簡單對比下STARK，STARK中每一行是一個約束，約束需要表示行與行之間的狀態轉換，但Plonkish中的自定義約束靈活性顯然更高。

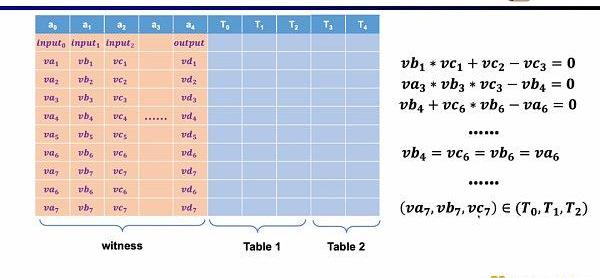
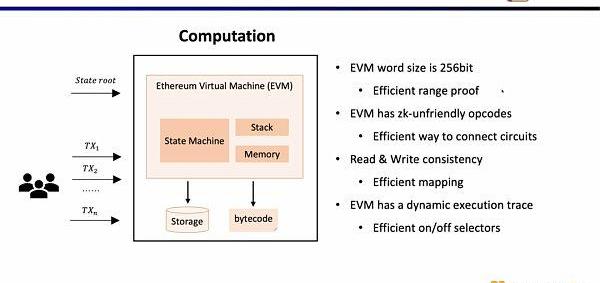
現在的問題是在zkEVM中，我們如何選擇前端。對于zkEVM主要有四個挑戰。第一個挑戰是EVM的字段是256位，這意味著需要高效得對變量進行范圍約束；第二個挑戰是EVM有很多ZK不友好的操作碼，因此需要非常大規模的約束來證明這些操作碼，例如Keccak-256；第三個挑戰是內存讀寫問題，你需要一些有效的映射來證明你所讀取的和之前所寫入的是一致的；第四個挑戰是EVM的執行蹤跡是動態變化的，因此我們需要自定義門來適配不同的執行蹤跡。出于上述的考慮，我們選擇了Plonkish。

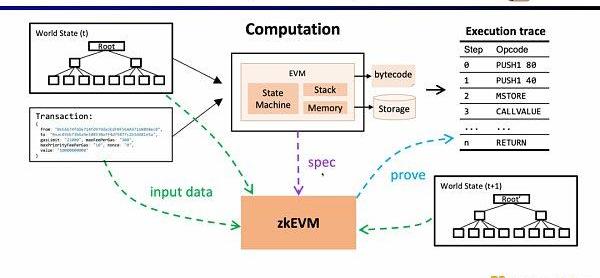
接下來，我們看zkEVM的完整流程，基于初始的全局狀態樹，一筆新的交易進來后，EVM會讀取存儲和調用的合約的字節碼，根據交易生成相應的執行蹤跡例如PUSH,PUSH,STORE,CALLVALUE，然后逐步執行更新全局狀態，得到交易后的全局狀態樹。而zkEVM是將初始的全局狀態樹，交易本身，以及交易后的全局狀態樹作為輸入，根據EVM的規范，來證明執行蹤跡的執行正確性。

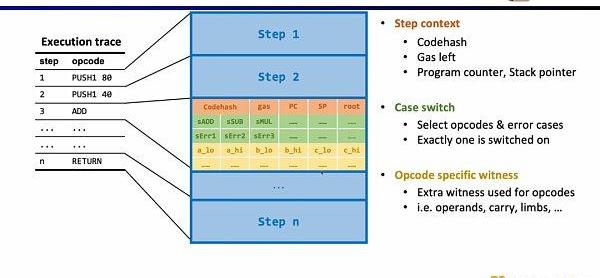
深入EVM電路細節，每一步執行蹤跡都有對應的電路約束。具體來說，每一步的電路約束包含StepContext，CaseSwitch，OpcodeSpecificWitness。StepContext包含執行蹤跡對應的codehash，剩余gas和計數器；CaseSwitch包含所有的操作碼，所有的錯誤情況，以及該步的相應操作；OpcodeSpecificWitness包含了操作碼所需的額外見證，例如運算數等。

醫療保健技術公司Prescryptive Health推出利用區塊鏈的平臺即服務:金色財經報道，醫療保健技術公司Prescryptive Health今天宣布推出其平臺即服務（PaaS），該服務將利用區塊鏈和人工智能的力量為藥房福利經理（PBM）提供實時服務。通過該服務，PBM可以為其成員提供相對透明的處方藥價格。該服務還可以讓PBM贊助商通過更低的藥品價格、更智能的計劃設計和更高的員工參與度節省高達40%的費用。[2021/10/27 21:00:00]

以簡單的加法為例，需要確保加法的操作碼的控制變量sADD設置為1，其他操作碼控制變量均為零。在StepContext中，通過設置gas'-gas-3=0來約束消耗的gas等于3，同理約束計數器，棧指針在該步后累加1；在CaseSwitch中，通過操作碼控制變量和為1來約束該步為加法操作；在OpcodeSpecificWitness中，對運算數的實際加法進行約束。

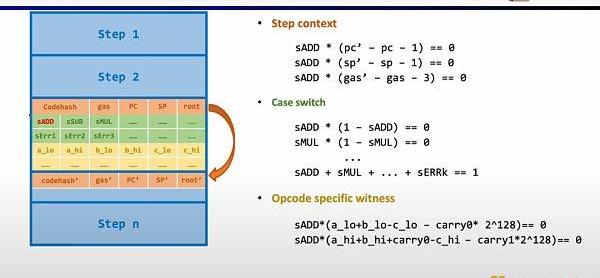
此外還需要額外的電路約束，來保證運算數從內存讀取的正確性。這里我們首先需要構建一個查找表來證明運算數屬于內存。并通過內存電路(RAMCircuit)來驗證內存表的正確性。

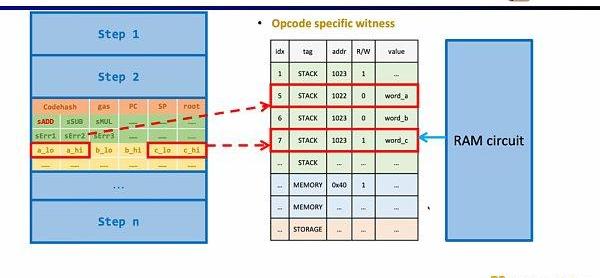
同樣的方法可以適用于zk不友好的哈希函數，構建哈希函數的查找表，將執行蹤跡中的哈希輸入和輸出映射到查找表，利用額外的哈希電路(HashCircuit)來驗證哈希查找表的正確性。

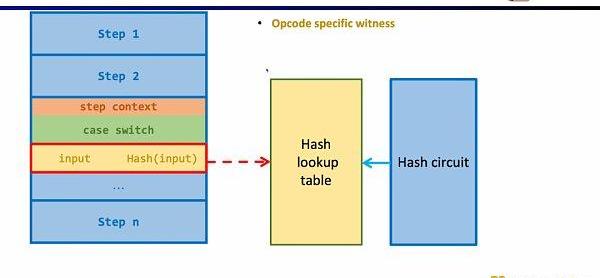
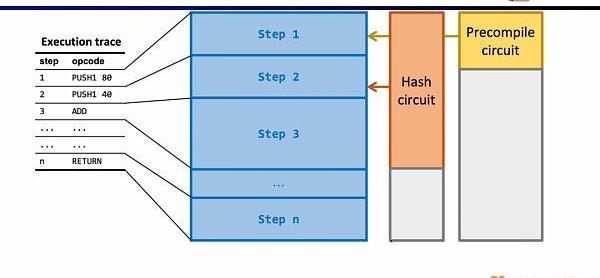
現在我們來看zkEVM的電路架構，核心的EVM電路用于約束執行蹤跡每一步的正確性，在一些EVM電路約束難度較大的地方，我們通過查找表來映射，包括FixedTable,KeccakTable,RAMTable,Bytecode,Transaction,BlockContext，然后利用單獨的電路來約束這些查找表，例如Keccak電路用于約束Keccak表。

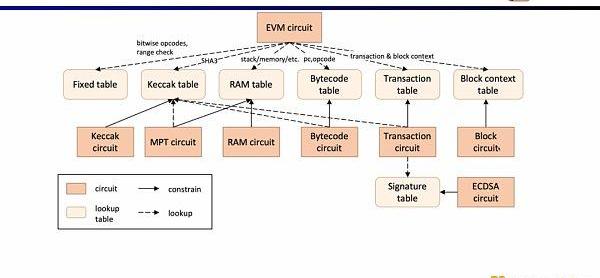
小結一下，zkEVM的完整工作流如下圖所示。

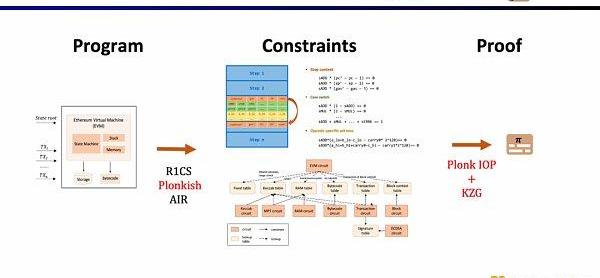
證明系統

因為在L1上直接驗證上述的EVM電路，內存電路，存儲電路等，開銷巨大，Scroll的證明系統采用了兩層架構。

第一層負責直接證明EVM本身，需要大量的計算來生成證明。因此第一層證明系統要求支持自定義門和查找表，對硬件加速友好，在低峰值內存下并行生成計算，且驗證電路規模小，可以快速驗證。有前景的可選方案包括Plonky2，Starky，eSTARK，它們前端基本上都使用Plonk，但后端可能使用了FRI，并且都滿足上述的四個特性。另一類可選的方案包括Zcash所開發的Halo2，以及KZG版本的Halo2。

TrustBase團隊完成subscript語言的Web3基金會Grant資助計劃項目交付:據官方消息，近日，波卡智能合約語言subscript的開發團隊成功向Web3基金會交付了subscript語言的核心庫功能。

subscript語言是由TrustBase維護的用于波卡wasm智能合約的語言框架，方便web開發者使用wasm智能合約構建DApp應用。開發團隊正在開發subscript合約語言的后續功能，完善波卡智能合約的應用生態。[2021/2/2 18:41:38]

還有一些新的證明系統也有很有前景，例如最近移除了FFT的HyperPlonk，而NOVA證明系統可以做到更小的遞歸證明。但它們在研究中只支持R1CS，如果他們未來可以支持Plonkish并且應用于實踐，將非常實用高效。

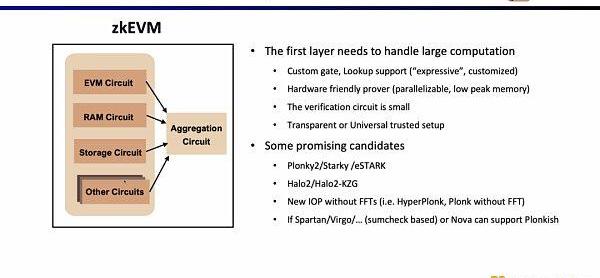
第二層證明系統用于證明第一層證明的正確性，需要可以在EVM中高效進行驗證，理想情況下，最好也是硬件加速友好并且支持transparent或者universalsetup。有前景的可選方案包括Groth16和列數較少的Plonkish證明系統。Groth16仍然是目前研究中證明效率極高的代表，而Plonkish證明系統在列數較少的情況下，也可以達到較高的證明效率。

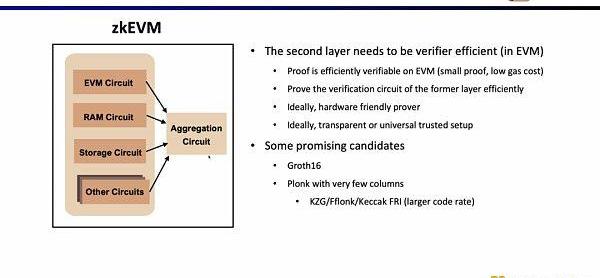
在Scroll，我們在兩層證明系統中我們都采用了Halo2-KZG證明系統。因為Halo2-KZG可以支持自定義門和查找表，在GPU硬件加速下性能良好，且驗證電路規模小，可以快速驗證。區別在于我們在第一層證明系統中我們使用了Poseidon哈希，進一步提高證明效率，而第二層證明系統因為直接在以太坊上驗證，仍然使用了Keccak哈希。Scroll也在探索多層證明系統的可能性，來進一步聚合第二層證明系統生成的聚合證明。

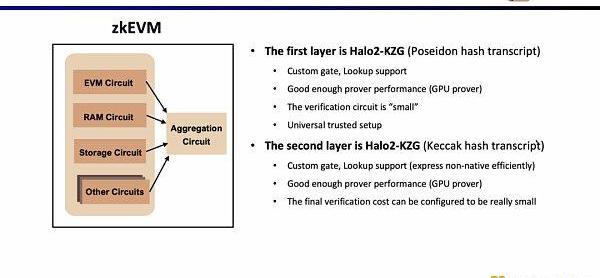
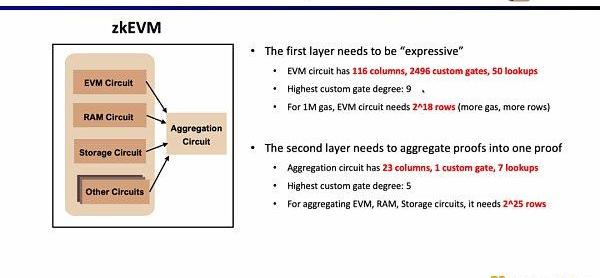
當前實現下，Scroll的第一層證明系統EVM電路有116列，2496個自定義門，50個查找表，最高階數為9，1MGas下需要2^18行；而第二層證明系統的聚合電路僅有23列，1個自定義門，7個查找表，最高階數為5，為了聚合EVM電路，內存電路，存儲電路，需要2^25行。

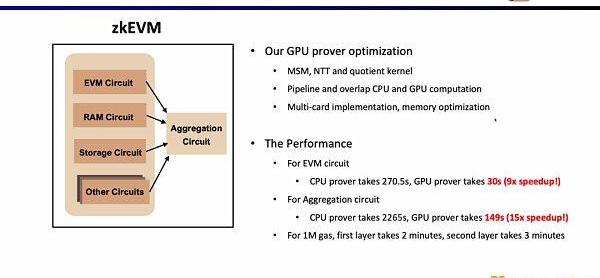
Scroll在GPU硬件加速方面也做了非常多的研究和優化工作，對于EVM電路，優化后的GPU證明者僅需30s，相較CPU證明者提升了9倍的效率；而對于聚合電路，優化后的GPU證明者僅需149s，相較CPU提升了15倍的效率。在當前的優化條件下，1MGas第一層證明系統大約需要2分鐘，第二層證明系統大約需要3分鐘。

有趣的研究問題

第三部分，張燁談論了一些Scroll在構建zkEVM過程中有趣的研究問題，從前端的算術化電路到證明者的實現。

電路

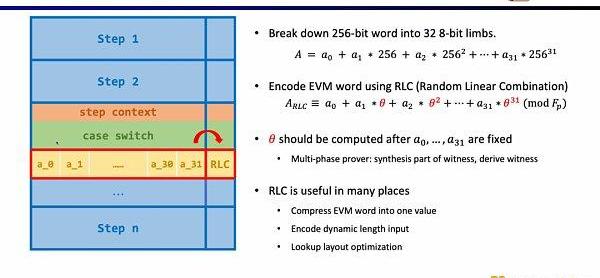
首先是電路中的隨機性，因為EVM字段是256位，我們需要將其拆分成32個8位的字段，從而更高效得進行范圍證明。隨后我們使用隨機線性組合(RandomLinearCombination,RLC)的方法，利用隨機數將32個字段編碼成1個，只需要驗證該字段就可以驗證原始的256位字段。但是問題在于隨機數的生成需要在拆分字段之后，才能確保不被篡改。因此Scroll和PSE團隊提出了多階段證明者的方案，來確保在字段拆分之后，再利用隨機數生成RLC，該方案被封裝在了ChallengeAPI中。RLC在zkEVM中有許多應用場景，不僅可以壓縮EVM字段成一個字段，也可以加密不定長的輸入，或是優化查找表的布局，但仍然有許多開放性的問題需要解決。

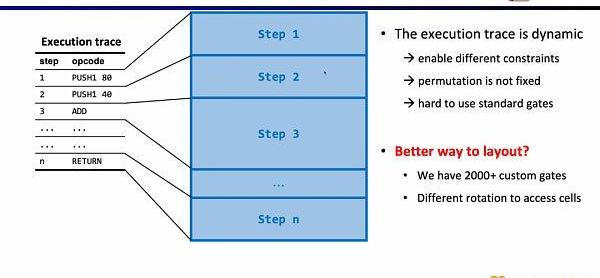
電路方面第二個有趣的研究問題是電路布局。Scroll前端之所以采用Plonkish，是因為EVM的執行蹤跡是動態變化的，需要能支持不同的約束，變化的等價性檢驗，而R1CS的標準化門需要更大的電路規模來實現。但Scroll目前使用了2000多個自定義門來滿足動態變化的執行蹤跡，也在探索如何進一步優化電路布局，包括將Opcode拆分成MicroOpcode，或是復用相同表格內的單元格。

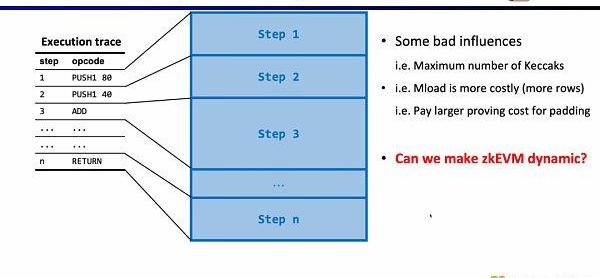
電路方面第三個有趣的研究問題是動態規模。因為不同的操作碼的電路規模不同，但為了滿足動態變化的執行蹤跡，每一步的操作碼都需要滿足最大的電路規模，例如Keccak哈希，因此我們實際上付出了額外的開銷。假設我們可以使zkEVM動態適應動態變化的執行蹤跡，這將節省不必要的開銷。

證明者

在證明者方面，Scroll在GPU加速上已經對MSM和NTT進行了大量的優化，但現在的瓶頸轉移到了見證生成和復制數據這塊。因為假設MSM和NTT占據了80%的證明時間，即使硬件加速可以將這部分效率提升若干個數量級，但原先見證生成和復制數據20%的證明時間將變成新的瓶頸所在。證明者的另一個問題是需要大量的內存，因此也需要探索更便宜更去中心化的硬件方案。

同時Scroll也在探索硬件加速和證明算法方面，來提升證明者的效率。目前主要有兩個大方向，或是切換至更小的域，例如使用64位的Goldilocks域，32位的梅森數等，或是堅持基于橢圓曲線的新證明系統，例如SuperNova。當然也有其他的一些別的可能路徑，歡迎有想法的朋友直接聯系Scroll。

安全性

在構建zkEVM時，安全性是至關重要的。PSE和Scroll共同構建的zkEVM有大約3萬4千行代碼，從軟件工程角度，這些復雜的代碼庫在很長一段時間內是不可能沒有漏洞的。Scroll目前在通過大量的審計，包括業內最頂尖的審計公司，來審核zkEVM的代碼庫。

其他使用zkEVM的應用

第四部分探討了其他一些使用了zkEVM的應用。

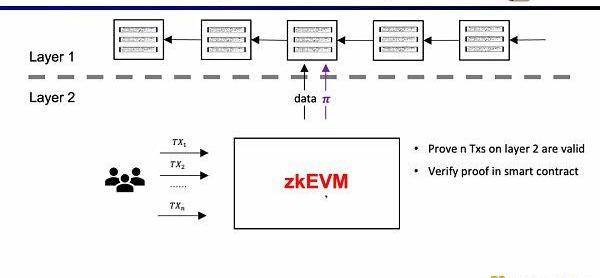
在zkRollup的架構中，我們通過在L1的智能合約，來驗證在L2上的n筆交易是有效的。

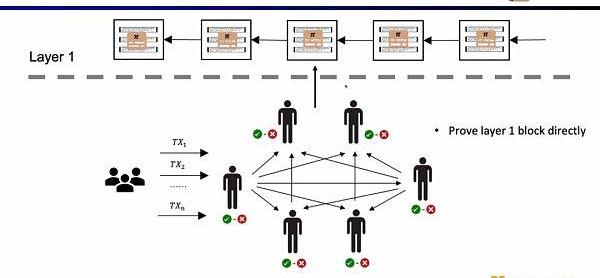
如果我們直接驗證L1的區塊，那么L1的節點就不需要重復執行交易，只需要驗證每一個區塊證明的有效性。這樣的架構方案稱為EnshrineBlockchain。目前在以太坊上直接實現難度非常之大，因為需要驗證整個以太坊區塊，其中會包括驗證大量簽名，隨之帶來更長的證明時間和更低的安全性。當然也已經有一些其他公鏈在通過遞歸證明，使用單個證明，來驗證整個區塊鏈，例如Mina。

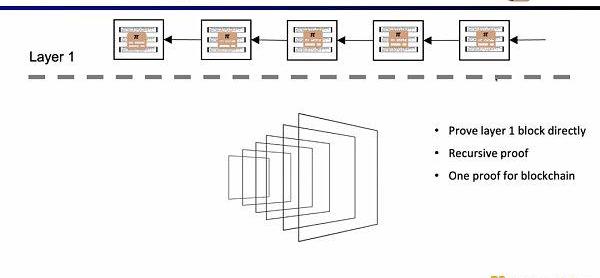
因為zkEVM可以證明狀態轉換，它也可以被白帽所利用，來證明自己知道某些智能合約的漏洞，尋求項目方的賞金。

最后一個用例是，是通過零知識證明來證明對歷史數據的聲明，作為預言機來使用，目前Axiom正在做這方面的產品。最近的ETHBeijing黑客松上，GasLockR團隊正是利用了這一特性，證明了歷史的Gas開銷。

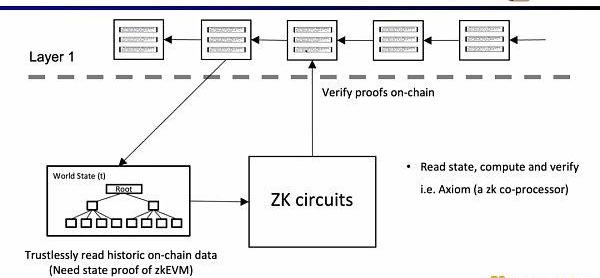
最后，Scroll正在構建zkRollup的以太坊通用擴容解決方案，使用了非常先進的算術化電路和證明系統，并且通過硬件加速構建快速的驗證器，證明遞歸。目前Alpha測試網已經上線，并穩定運行了很長時間。

當然仍然有一些有趣的問題需要解決，包括協議設計和機制設計，零知識工程和實際效率，歡迎大家加入Scroll一起構建！

來源：panewslab

原文：YeZhang

編譯：F.F

Tags：SCRROLROLLCRODMScriptThe Troller CoinCROP價格

火必