區塊鏈:密碼學研究 | 動手計算雙線性對（上）_curve幣價格走勢

零知識證明是重要的密碼學技術之一，其中基于電路的通用零知識證明算法更是因為近年取得的長足發展和在區塊鏈項目中的應用而備受關注。雙線性映射，也叫雙線性配對或雙線性對，是通用零知識證明算法的重要組成部分，也是眾多密碼體制，如聚合簽名、身份基加密、屬性基加密等的關鍵構件。本文從零基礎開始，通過完整的模擬雙線性對的原理來實現一套在小有限域上的雙線性映射，幫助讀者加深對雙線性映射的理解。

“動手計算雙線性對”這個系列計劃有上中下三篇內容，本文是上篇，介紹后面文章需要的一些基礎知識。在中篇，我們將對一個名為curve101的曲線進行討論，其有限域只涉及101個元素，用于配對的橢圓曲線子群只有17個點，不借助計算機也能方便的通過純手算完成整個過程，十分適合零基礎讀者入手。下篇則會實際計算并討論雙線性對的實際例子，全部的中間計算過程我們都將列出，讀者可以按步驟重現整個計算流程。

在之后介紹零知識證明算法的系列文章中我們還會用到這個curve101進行演示，屆時讀者可以更加明白雙線性對的作用，而接下來我們就來一起從零基礎開始演算這個雙線性曲線。

動態 | 量子鏈開發者在密碼學IACR電子期刊公布幻影隱私協議:金色財經報道，2月13日，量子鏈開發者在密碼學IACR電子期刊公布了基于智能合約的幻影隱私協議（Qtum Phantom Protocol），推動數字資產隱私領域發展。據介紹，幻影隱私協議基于zk-SNARK技術，對Merkle樹、hash算法等多個環節進行了改進，使得協議能夠高效地運行于智能合約上。量子鏈幻影隱私協議在智能合約的基礎上，實現隱私資產的發行和管理。相比AZTEC只能實現交易金額的隱私，無法隱藏交易地址。幻影協議實現了更徹底的隱私，可以同時隱藏交易金額和交易地址。該協議同時提供隱私資產和公開資產之間的互轉功能。據悉幻影隱私協議將率先在Qtum網絡部署，同時也計劃支持其他的智能合約網絡。[2020/2/14]

眾所周知，很多公鑰密碼體制都是建立在有限域上，特別是模素數的有限域。作為零基礎的系列，我們不去糾結數學概念“域”的嚴格定義，而是通過介紹帶模運算相關的內容，來真實的展現一個有限域。

聲音 | 中國傳媒大學計算機學院副教授：區塊鏈反過來激活了數學和密碼學的新應用:在11月8日由中國人民大學國家版權貿易基地主辦的“區塊鏈技術與版權保護”研討會上，中國傳媒大學計算機學院副教授姜正濤從密碼學角度解讀了區塊鏈與版權保護之間的關系。他表示：“密碼學過去是‘賠錢’的技術，屬于純開銷。有了區塊鏈之后，計算結果本身就有價值，比如電子貨物、比特幣、版權信息等本身就具有價值，所以區塊鏈反過來激活了數學和密碼學的新應用。”而且，區塊鏈可以記錄所有發生的交易，可以有效避免造假。另外，區塊鏈對低價值、實時產生的版權數據記錄的成本比較低，相較于傳統做法，區塊鏈可以節省權利人提交材料、等候審批的人力物力，對于作品價值比較低但是數量大的作品，可以提供較好的保護渠道。[2019/11/21]

帶模運算是在我們熟悉的加法和乘法的基礎上增加一步計算余數的操作，例如，在以7為模數的系統中：

3+3=6，也就是mod7=6

3+6=2，也就是mod7=2

動態 | 谷歌將采用密碼學以保持數據集的私密性:據wired報道，谷歌將發布一個名為Private Join and Compute的開源加密工具。它有助于連接來自不同數據集的數字列，以計算在整個數學過程中加密和不可讀數據的總和，計數或平均值。只有計算結果才能被所有各方解密和查看 - 這意味著你只能獲得結果，而不能獲得你未擁有的數據。該工具的加密原理可以追溯到20世紀70年代和90年代，但谷歌已經重新利用并更新它們，以便與當今功能更強大、更靈活的處理器配合使用。[2019/6/21]

4×2=1，也就是mod7=1

所謂模素數就是說取模操作針對的是某個素數p，例如上述的7，或者curve101中的101。p是素數這個細節是關鍵的，在下文介紹帶模乘法的逆運算時你將會對這一點的必要性有更深的體會。

有了模加法，我們可以定義其逆運算是模減法，例如：

6-3=3，也就是mod7=6

2-6=3，也就是mod7=3

聲音 | 肖風：密碼學已在理論上有很多成果可供解決數據隱私保護問題:今日在“Web 3.0時代隱私計算構建新數據共享世界”峰會上，萬向區塊鏈董事長肖風表示，隨著人工智能的興起，隱私計算成為世界性話題。然而，并非所有數據都存在于互聯網平臺上，也不是所有數據都是法律法規允許共享的。因此隱私計算的概念才得以提出，而恰恰密碼學已在理論上有很多成果可供我們來探討解決數據隱私保護問題。[2018/12/1]

同理，有了模乘法，自然而然會想到去定義其逆運算“模除法”。但是加、減、乘我們可以直接正向計算得到，“模除法”就比較困難。例如為了求3/2等于幾必須思考哪個數乘以2等于3，而這個思考過程并不是特別直接。好在我們模7的例子中涉及到的元素并不多，因此通過窮舉就能找到答案：因為2×5=3，所以3/2等于5。

需要注意到3/2其實可以轉化為3×(1/2)，而因為剛才我們計算過4×2=1，所以1/2的值我們其實是知道的。因此3/2=5可以通3×4=5計算出來。這啟發我們可以枚舉全部形如1/n的數得到一個“倒數表”，然后借助“倒數表”將除法轉化為乘法進行。

現場 | 姜海：密碼學將隨著黎曼猜想等理論研究的深入迎來大發展:金色財經現場報道，今日，2018可信區塊鏈峰會在北京召開。在主題為“區塊鏈安全焦點關注”的區塊鏈安全論壇上，丁牛科技有限公司CEO姜海結合最近黎曼猜想被證明引起了密碼學界的高度關注，分析了黎曼猜想與區塊鏈密碼安全。他提出，盡管黎曼猜想的證明對于傳統密碼安全有極大的沖擊，但是區塊鏈技術的安全建立在SHA-256、橢圓曲線、算法校驗等基礎之上，在使用過程中能夠極大地抵抗密碼攻擊。盡管最近有很多的安全事件發生，而其根本原因在于程序的違規操作。未來隨著隨機發生器、量子計算機以及黎曼幾個等基礎理論的研究，密碼學將會有更大的發展空間。[2018/10/10]

模7逆元表

按習慣，我們一般不用1/n的寫法，也不用“倒數”這個稱呼。而是將1/n寫做?n-1，并將其稱為n的逆元。下文我們將遵從習慣，使用逆元這個叫法。顯而易見的是，在不同的模系統中，同一個數的逆元是不同的。比如模7系統中，3的逆元是5；而模11系統中3的逆元是4。因此除非有明確的語境和上下文，否則為了避免歧義，還要說明逆元是模幾的逆元才有意義，比如一個完整的說法是：3的模7逆元是5。

在模7的系統中，我們為每個元素都找到了逆元，在模17和模101的系統中也可以完成這樣的操作。那么我們自然而然會想：是否在任何模的情況下都能為每個元素找到逆元呢？答案是否定的，例如在模8的系統中，找不到任何一個數乘以2等于1，也就是說在模8的系統中計算1/2這個“除法”是沒有意義的。實際上，只有在模為素數的情況下才能為每個元素都找到逆元，也就是說在模素數的情況下我們才可以給任意兩個元素計算“除法”。在這樣的模素數系統中，任意兩個元素都能完成加減乘除四則運算，我們稱模7加法、模7乘法和集合{0,1,2,3,4,5,6}組成一個有限域：模7剩余類域。

所謂“有限”的意思就是集合的元素是有限的，比如這里的7個元素。雖然在本篇科普性質的文章對待數學概念都并非十分嚴格和謹慎，但是這里仍然能夠揭示域的一些關鍵性質。比如我們發現僅利用集合中的元素就能夠計算四則運算。模7剩余類域是這樣，有理數域、復數域等也都是這樣，意識到這一點就已經足夠完成后面文章的閱讀了。我們后面用Fp代指模p剩余類域，例如F7，F101等。

討論完了加減乘除四則運算，按照我們曾經學習有理數的思路，我們來考慮開平方運算。例如3×3mod7=2，所以3是2的“平方根”。如果某個非零元素是可以開平方根的，我們稱這樣的元素為模7的二次剩余，否則就叫模7的二次非剩余。這樣我們可以列出下面一張表：

可以注意到，二次剩余的個數和二次非剩余的個數是相等的，二次剩余的逆元仍然是二次剩余，二次非剩余的逆元也仍然是二次非剩余；而且我們還注意到，每個二次剩余都有兩個根并且他們的和為0，這一點性質像極了正實數：正實數的平方根總有兩個，他們互為相反數。

如何判定一個數是否為二次剩余和如何求二次剩余都是有趣和實用的問題。比如在動手計算雙線性對會談到的橢圓曲線中，已知x坐標和橢圓曲線方程求y的過程就需要考慮計算二次剩余的問題。相關的方法一般會涉及到勒讓德符號等。而在我們的討論的例子中因為元素的數量很少，我們一般采用窮舉的方法就能解決。

經過上面的演算，我們發現3在F7中沒有“平方根”，也就是不存在某個數其平方模7為3。類比復數域對實數域的擴展，我們假設3的一個平方根為j，即j*jmod7=3。現在我們把j加入到{0,1,2,3,4,5,6}集合中，然后嘗試再加入一些其他元素使得新的集合仍然構成一個域。

首先為了能夠計算加法和減法，至少還要加入j、1+j、2+j、3+j、4+j、5+j、6+j，為了能夠計算乘法我們至少還要加入j、2j、3j、4j、6j、6j，最終我們發現一個新的能夠計算四則運算的集合至少要有下面49個元素：

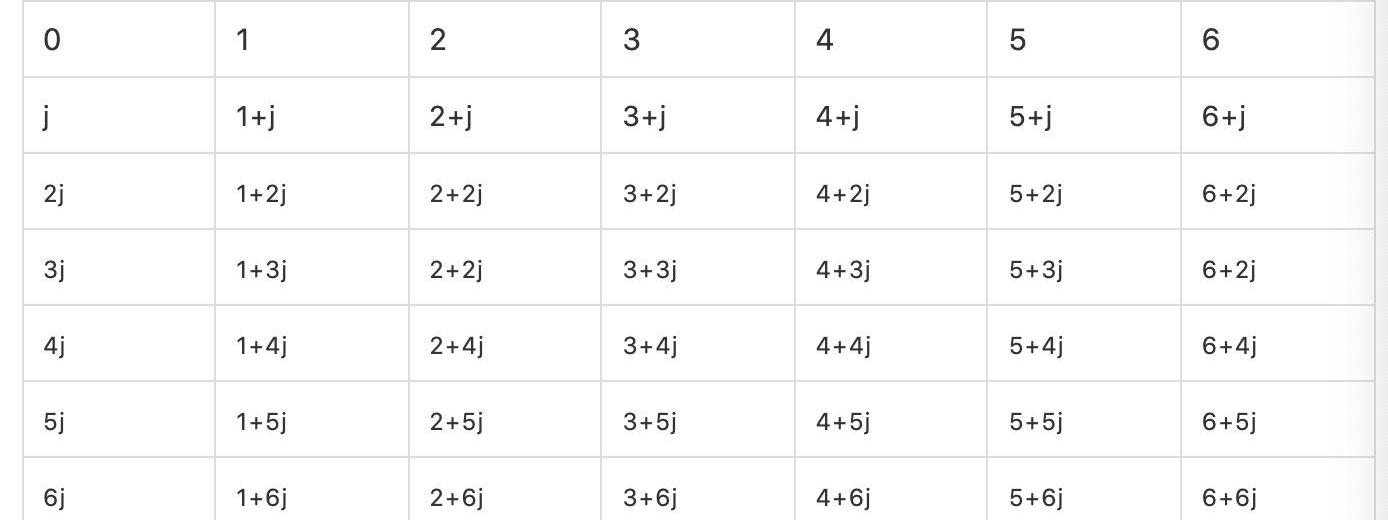
例如6j+j=0；(3+j)(5+2j)=4j;(4+4j)-1=6-6j

那么僅用這49個元素能夠完成四則運算嗎？答案是肯定的，雖然本文不去嚴格證明這一點，但是可以簡單揭示一些其中的原因：

對于加法和減法，我們很容易驗證任意兩個元素的和、差都在還在集合中；對于乘法，因為j×j=3這條規則，簡單驗證后我們就能發現任何兩個元素的積還是在集合中；唯一需要仔細考慮一下的是除法；對于除法，我們總可以通過如下方式計算a+bj的逆元：

因為a和b是F7中的元素，因此a2-3b2?也是F7中的元素，因此可以判定a2-3b2?的逆元仍然是{0,1,2,3,4,5,6}中的元素。所以最后可以發現a+bj的逆元是(a-bj)(a2-3b2)-1，它仍然落在49個元素之中。所以新的49個元素組成的集合不但包含{0,1,2,3,4,5,6,j}，而且能夠計算四則運算。這個新的集合其實也是一個有限域，我們稱其為F7的二次擴域，記為F72，之所以是“二次”，我們可以這樣粗暴的理解：每個F72中的元素需要兩個F7的元素通過組合的方式來表示。

本篇介完了關于模運算和模p剩余類域的一些基礎知識，下一篇“動手計算雙線性對”，我們會介紹關于有限域上橢圓曲線的一些例子和知識，屆時會使用到本篇中的內容，敬請期待。

作者簡介

喬沛楊趣鏈科技基礎平臺部區塊鏈底層密碼學小組

Tags：區塊鏈MODCurve量子鏈區塊鏈技術發展現狀和趨勢MODA價格curve幣價格走勢量子鏈幣最新消息

中幣