LON:【密碼專欄】超強進階：PLONK VS Groth16（上）_Deri Protocol

前言

前文《天冷了，干了這碗“零知識證明”雞湯》對「零知識證明學習」作了一個形象化的比喻：燉雞湯。那么本系列的主要內容可以簡單概括為《論高壓鍋燉雞湯的一百種方法》之方法二。在學會了“清燉雞湯”之后，不如來一口“阿膠雞湯”補補腦細胞吧！

正如雞湯不同風味之間各具千秋，不同的zk-SNARK方案也各有所長。zk-SNARK方案可以被分為與zk-SNARK，PLONK與Groth16分別是其中的典型代表。通過本系列，我們將對PLONK算法內容作簡要介紹，并指出PLONK和Groth16算法思路上的異同。

PLONK算法在中提出，由來自于ProtocolLabs的研究員Gabizon和以太坊隱私交易協議AztecProtocol的兩名研究人員合作完成。PLONK的提出晚于Groth16，在證明和驗證的性能上與Groth16也存在一定差距，但是基于通用可更新的可信設置這一特點，使PLONK算法在零知識證明領域占據了一席之地。

可信設置

可信設置可以說是PLONK和Groth16兩者間最顯著的差異。正是為了避免一次性的可信設置，PLONK設計了后續的約束系統和問題壓縮方式。那么什么是零知識證明中的可信設置呢？可信設置實際上是在創建一個用于證明驗證的秘密，任何知道這個秘密的人都可以偽造證明通過驗證。如果將零知識證明看作是一扇擋在證明者a和驗證者b之間上鎖的門，那么合法構建的證明就是可以打開門的口令，a提供口令即可進入房間。但是如果a得知了門的秘密也就是房間窗戶的位置，那么a可以直接無視鎖的存在翻窗進入房間。

Web3游戲Cat Paradise以1500萬美元的估值完成近100萬美元種子輪融資:金色財經報道，基于TON開發的Web3游戲Cat Paradise宣布完成種子輪融資，該輪融資以1500萬美元的估值募集了近100萬美元資金，Mask Network、Moon Capital等機構參投。該公司將利用這筆資金改進現有的鏈上技術，聘請更多熟練的開發人員，并接觸更多的客戶。Cat Paradise是一款數字貓寵物養成類游戲，由游戲開發商Pluto Games開發。[2023/6/20 21:47:56]

▲無窗的房間

顯然，最安全的做法是找一個「沒有窗的房間」，這也是一部分零知識證明方案的思路——無需可信設置，例如可擴展透明知識論證zk-STARKs和防彈證明Bulletproofs。雖然它們的安全性得到提高，但是目前這類方法的證明驗證性能是遠低于zk-SNARKs的，近線性的驗證和規模較大的證明使其不適用于很多場景。

▲窗戶位置指定策略

PLONK和Groth16的做法都是保留窗戶，但是盡力保護窗戶的位置不被別人知道。

Groth16的做法是：根據不同的問題，每次都指定窗戶在房間中的擺放位置，也就是它需要一次性的可信設置。而PLONK面對不同的問題時：窗戶的位置是固定不變的，即窗戶的位置只需要被指定一次。也就是說PLONK的可信設置是通用的。那么這些窗戶指定的位置由誰來確定呢？當然，可信第三方是一個備選項。但這意味著說這間房間是否會被惡意證明者攻破，其安全性寄希望于這位第三方。除此之外還有一項熱門技術也可為其提供思路——多方安全計算。沿用之前的例子，可以不太嚴謹地將MPC概括為：多個人共同指定窗戶的位置，除非這些參與者全部聯合起來對答案，這個位置將無法由任何人得知。

利物浦大學擬構建首家基于元宇宙和區塊鏈技術的國家數字遺產研究中心:金色財經報道，利物浦大學虛擬工程中心 (VEC)宣布已獲得100萬英鎊投資，這筆資金用于建立英國第一個國家數字遺產研究中心并創建數字遺產生態系統和戰略，通過人工智能、區塊鏈和元宇宙等技術促進和發展文化遺產，利用數字技術來增進對文化和自然遺產的理解和保護。（liverpoolexpress）[2023/5/22 15:19:09]

顯然，使用MPC時，參與者的數量越多，秘密的安全性越高，這類可信設置也比可信第三方更為用戶所接受。遺憾的是，雖然目前提出了基于Groth16的可信設置，但是由于Groth16的秘密計算與特定的問題相關聯，每次遇到新的問題時，必須重新開啟一輪MPC可信設置。可想而知，需要多方參與的計算協議將是極為繁瑣的，這樣將大大影響Groth16的性能。相比之下，具備通用性的PLONK與MPC的適配度極高。

而之前提到的PLONK可信設置的可更新性則是指：通用的PLONK秘密可以通過再開啟一輪MPC作更新。新生成的秘密安全性建立在兩次MPC的安全性上，只要兩次中有一個參與者是誠實的，這個秘密就是可信的。約束系統

Groth16及PLONK均將程序先轉化為一個由加法門和乘法門組成的算術電路，再通過將電路構建為多項式的形式來進行后續的計算。本節我們將使用Vitalik文章中的一個簡單例子進行說明：

Glassnode：幣安在過去30天里流出32億美元的穩定幣:金色財經報道，在Glassnode追蹤的所有交易所中，穩定幣在過去30天里累計流出48億美元，其中幣安流出32億美元，占穩定幣流出量的66%。[2022/12/16 21:48:09]

對于程序qeval,prover需要證明自己知道qeval(x)=35的解，即x=3。

defqeval(x):

y=x**3

returnx+y+5，其轉化為算術電路可表示如下：

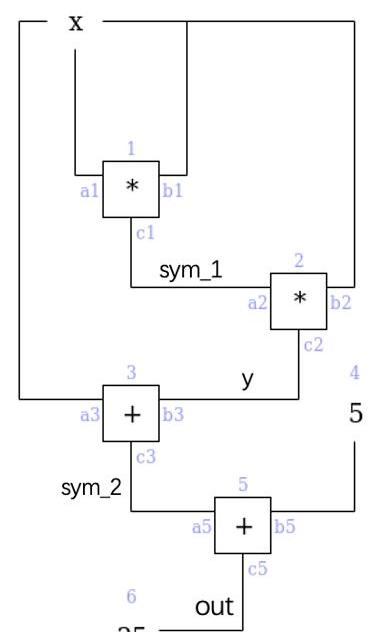
PLONK中，上圖電路的描述由兩部分組成：門約束與線約束。門約束固定電路中每個門的動作。此外，在電路中我們規定相連線的值應保持一致，對此線約束規定這些線的關系。接下來我們分別討論兩類約束的多項式表示。門約束

在PLONK中，對于第i個門，可被描述為如下形式：

（QLi)ai+(QRi)bi+(QOi)ci+(QMi)aibi+Qci=0

其中Q均為常數，a,b,c則是信號的下標。具體地，在PLONK中門約束可以被分為三類：算術約束、布爾約束、公共輸入約束。

英超埃弗頓足球俱樂部推出數字球衣NFT:8月2日消息，英超埃弗頓足球俱樂部宣布與NFT初創公司Fancurve合作推出數字球衣NFT，這些數字球衣將在元宇宙虛擬世界中提供給數字化身使用。據悉，該NFT將由Fancurve的內部3D時裝設計師團隊設計，且被定位為高端數字藏品。（Sports Pro Media）[2022/8/3 2:54:47]

最為常見，用于表示電路中的所有加法門和乘法門，此時a,b,c分別表示門的左右輸入和輸出信號下標，Q_C一般為0。根據門的類型剩余的符號有不同的取值：

加法門：QLi=1，QRi=1，QOi=-1，QMi=0??ai+bi-ci=0乘法門：QLi=0，QRi=0，QOi=-1，QMi=1-ci+?aibi=0

顧名思義，用于約束布爾類型的信號，其值只能取0或1。例如現在需要約束下標為j的信號∈{0,1}，那么門約束式子中各變量的取值為：

ai=bi=j，QLi=-1，QMi=1，QOi=QRi=Qci=0

-j+j*j=0

另外，針對問題中出現的證明方和驗證方都知道取值的輸入，需要在約束系統中有所體現。例如要求約束下標j的信號取值為v，對應的取值為：

《堡壘之夜》開發商：為了元宇宙的開放，將與蘋果和谷歌戰斗到底:金色財經報道，《堡壘之夜》開發商Epic Games首席執行官蒂姆·斯威尼 (Tim Sweeney)在接受英國《金融時報》采訪時表示，科技巨頭蘋果和谷歌可能會不公平地擴大對智能手機平臺的束縛，以主導所有在虛擬環境中進行的交易。蒂姆·斯威尼表示，網路游戲《堡壘之夜》可以說是當今最接近元宇宙的東西。每個月約有7千萬玩家沉浸在其數字世界中，參與大逃殺 (Battle Royale)戰斗，他絕不允許科技巨頭像在智慧手機應用程序上那樣，利用壟斷力量主導新平臺，為了元宇宙的開放將與蘋果和谷歌戰斗到底。[2022/6/1 3:55:36]

ai=j，QLi=1，QMi=QOi=QOi=0，Qci=-v

j-v=0

利用該式，我們可以很容易地表示上圖中的所有門約束：

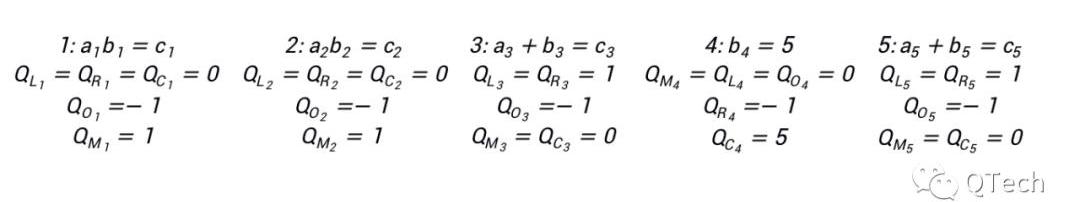
與Groth16類似，可以將所有的多項式組整合在一個多項式中：

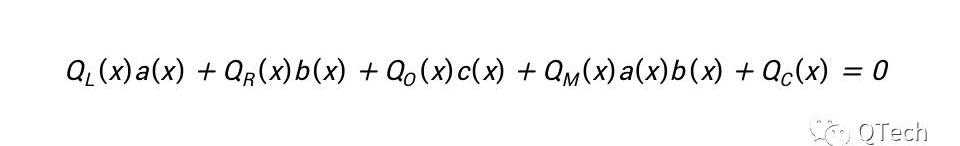
線約束

線約束可以分為兩種情況：

同一多項式內部，例如：a1=a3

不同多項式之間，例如：a1=b1

當只需要考慮情況1時，可以通過構造p(x)=P(x)來實現約束：

X(X)=X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

其中β,γ為隨機數，X->Y表示了待約束的多項式，P(x)使用了x的置換σ(x)。對于下面例子：

X(1)→Y(1)

X→Y：X(2)?→?Y(2)?and，Y(1)=Y(3)

X(3)→?Y(3)

σ(1)=3

σ(X)：σ(2)=2

σ(3)=1

當且僅當Y(1)=Y(3)成立時，p(x)=P(x)。

現在，讓我們增加問題的復雜度：需要約束的多項式個數為k時。自然地，設門的總數為n，我們可以對第j個多項式構造對應的p_j(x)=P_j(x)，即

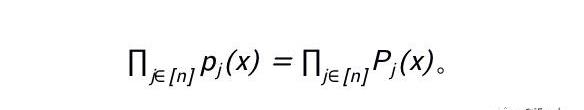
進一步地，情況2的出現要求對以下情況中的x作區分：

pj(x)and?pi(x)????

那么可以增加對x的映射，對于第j個多項式：

X(X)=(j-1)*n+X

p(X+1)=p(X)*(β*X(X))+Y(X)+γ）

P(X+1)=P(X)*(β*X(σ(X))+Y(X)+γ）

p(0)=P(0)=1

以上就是線約束的全部內容，其實質是為了保證電路中同一條或相連線上的值相等。

與Groth16類似，將上述的約束聯立將得到一個完整的PLONK約束系統。通過將抽象的代碼和電路轉化為約束系統R1CS，我們可以將一個零知識證明問題固定下來。讓我們帶著問題進入下篇：PLONK中如何將R1CS轉為多項式描述？它與Groth16做法區別在何處？敬請期待！

ArielGabizonandZacharyJ.WilliamsonandOanaCiobotaru.(2019).PLONK:PermutationsoverLagrange-basesforOecumenicalNoninteractiveargumentsofKnowledge.

SeanBoweand?ArielGabizonandIanMiers.(2017).ScalableMulti-partyComputationforzk-SNARKParametersintheRandomBeaconModel.

https://vitalik.ca/general/2019/09/22/plonk.html

Tags：LONPLOROTGROpoloniex交易所官網PLOCKDeri ProtocolStickman Battleground

萊特幣