ZKP:輕松讀懂零知識魔法_QUO

零知識證明是一種魔法。它能讓我們做到以前想都不敢想的事情。

首先，讓我引用幾句名言來刺激你的大腦。有些可能是你耳熟能詳的，有些可能是你第一次聽說。

神奇的技術、不斷進步的文明、簡短的文字、隱私以及已經到來的未來。這就是零知識證明（ZKP）。這是怎么回事？

上個世紀，計算機和互聯網席卷了整個世界。這些技術無處不在，我們所做的一切都離不開它們，無論好壞。在此基礎上，我們建立了平臺、公司和巨頭。這些就像你的 MAMAA（微軟、蘋果、Meta、Alphabet、亞馬遜）。然后是巨頭的腹部 --支付網絡、政府服務和大量的 B2B 應用程序，它們默默地運行著這個世界。最后，還有一條長尾應用 -- 可愛的濾鏡圖片應用、語言學習平臺或在線社區。

當你向另一個在線服務輸入數據時，你期望實現一個特定小目標，比如聯系朋友，或者是申請抵押貸款這樣的大目標。但所有這些數據會發生什么變化呢？還有你不知道的冰山一角的隱藏數據。

誰真正了解這些系統以及我們如何使用它們的后果？反過來，它們又是如何利用我們的？雖然有些人可能比其他人更了解某些系統，但沒有人了解所有系統，更不可能了解它們是如何相互作用產生不可預見的后果的。

人類該怎么辦？信任, 但你相信誰呢？

這是一個難題。我們人類的大腦還沒有進化到可以思考這個問題的程度。互聯網雖然能把我們聯系在一起，讓事情變得更簡單，但也在這方面卻造成了一些混亂。過去，當你與人私下交談時，風會吹走你發出的聲音。當你被鎖在屋外時，你可以找鎖匠，也可以自己撬鎖。當你被鎖在谷歌賬戶外，盯著 "拒絕訪問 "的屏幕時，你能怎么辦，你正站在一座無形而堅不可摧的城堡前。

ZKP 可以幫助你。也許不是任何事情都可以搬到你，也不是此刻。但它可適用于許多事情、許多地方，而且越來越多。在本文的其余部分，我將嘗試說服你為什么以及如何做到。讓我們跟隨魔法的腳步。

本節將介紹零知識證明的概念

這是關于零知識證明及其應用系列文章的第一篇。我們將介紹什么是零知識證明、為什么你應該關注它、它是如何工作的，以及它的應用場合。

想象一下，你去酒吧，可以證明自己年滿 18 歲，而無需透露任何其他信息，包括帶有個人信息的身份證。或者，你可以證明自己正確繳稅，而無需向任何人透露你的收入或資產詳情。這些都是零知識證明（ZKP）可以實現的。所謂 "零知識"，簡單地說就是我們不會透露任何超出預期的信息。

ZKP 可以讓你在不透露任何信息的情況下證明某件事情，只需證明該聲明是真實的即可。

這意味著什么呢？讓我們以經典的 "沃爾多在哪里 "為例。這個游戲是關于在一幅大圖中找到沃爾多。我可以向你證明我知道沃爾多在哪里，而不透露沃爾多的位置。怎么證明？

想象一下，我有一張 "沃爾多在哪里 "的圖片和一張比圖片大四倍的大紙。我在紙上開一個小洞，然后把這張紙放在 "沃爾多在哪里 "圖片的前面，小心地擺好位置，這樣沃爾多就可以通過小洞看到了。這意味著你可以看到瓦爾多，但只能看到瓦爾多，看不到其他東西。這樣，你就知道我知道沃爾多在哪里，但我并沒有透露沃爾多在圖片中的具體位置。

這顯然只是一個例子，但希望它能給我們一些直觀的印象，讓我們知道這樣的證明是如何實現的。但這意味著我們要更精確地要證明什么？我們接下來會深入探討這個問題，但現在讓我們看看 ZKP 給我們帶來了什么。

有了 ZKP，你就能以通用的方式證明任意語句。更具體地說，ZKP 能讓我們以一種私密而簡潔的方式證明一些東西。

這一點非常強大，我們接下來就會看到。

本節將解釋為什么有人會關注 ZKP，包括詳細介紹隱私、壓縮和 ZKP 的通用性。

讀了上面的內容，你可能會想："好吧，我想這還挺不錯的，但我為什么要關心呢？這種想法完全合理。事實上，你可能不應該關心！就像你不應該關心計算機的工作原理、人工智能的發展方向或其他任何事情一樣。

為什么你會關心？因為你很好奇，想了解 ZKP 是如何工作的，以及它能開啟哪種類型的交互。這種機制非常普遍，許多在這一領域工作的人的直覺是，從根本上說，它是一種新的范式，可以釋放出許多新的東西。我們已經看到了這一點，而且似乎我們才剛剛開始。在本節的其余部分，我將向你介紹一些直觀的原因和方法。

在深入探討之前，讓我們先從更高的層面了解一下 ZKP 給我們帶來了什么。ZKP 主要具有以下一種或兩種特性：

1.隱私（更正式的說法是零知識性 zero-knowledge）

2.壓縮（更正式的說法是簡潔性 succinctness）

這兩個概念是什么意思？下面是一些思考這些特性的方法。

有很多事情我們都想保持隱私。下面是《牛津詞典》中 "隱私"的定義：

只屬于一個人或一群人，或僅供他們使用。

我們有私人談話、私人浴室、隱私部位。商業秘密、敏感的個人信息，在自己家中的隱私：鑰匙、門和鎖。

ITM Trading分析師：CBDC將允許輕松跟蹤用戶的資金和消費習慣:金色財經報道，ITM Trading首席市場分析師Lynette Zang表示，由于國會通過的立法，美國銀行有權沒收人們的資金。在最近的一次采訪中，Zang討論了美元的購買力如何下降到“大約三美分”，她相信中央銀行數字貨幣 (CBDC) 將加強“監督經濟”，以及世界經濟的不可改變的性質論壇的提議，被稱為大重置。Zang就央行數字貨幣 (CBDC) 的潛在危險發出了警告。她認為，這些數字貨幣將允許輕松跟蹤用戶的資金和消費習慣，以及凍結這些資金的能力。Zang將CBDC視為世界經濟論壇提議的大重置的一部分。她認為，財富永遠不會消失，而只會轉移位置，如果一個人不擁有它，其他人就會擁有，你可能什么都沒有，但我敢肯定你不會快樂，因為你會租用所有東西。[2023/2/11 12:00:12]

隱私是正常的，它就在我們身邊。它與自我主權、自決和獨立的概念密切相關。這些概念對我們來說是如此自然，以至于許多重要文件，如《美國權利法案》和《聯合國憲章》分別將其視為個人和國家的基本權利。隱私是自由的前提。

更正式地說，ZKP 的隱私屬性通常被稱為*零知識*或*數據隱藏*。ZKP 隱藏了與某些應用功能無關的數據，然后將被隱藏過這些數據與相關應用數據綁定在一起。這些概念比較正式，可以實現隱私保護。隱私是一個更廣泛、更普遍適用的概念，所以我們現在將繼續關注這個概念。

在數字世界（也稱網絡空間，與肉體空間相對）中，隱私也是至關重要的，但卻常常被忽視。以下是《賽博朋克宣言》（_A Cypherpunk's Manifesto_ ）中對隱私的定義：

隱私是有選擇地向世界展示自己的能力 by 《賽博朋克宣言》

對話、密碼、信用卡信息。這些都是我們希望在網上保持隱私的例子。互聯網是連接我們所有人的奇妙工具，但它也是一個開放而狂野的海洋。這里有很多陌生人和掠奪者，因此保持某些信息的私密性至關重要。

你可能會想，"我們已經可以將密碼等信息保密了，有什么大不了的？在有限的意義上，就這些具體例子而言，你是對的。我們必須發揮更多的想象力，才能真正理解通用的可編程隱私功能。

舉個例子，想一想奧古斯丁在他的《懺悔錄》(公元 400 年)中是如何發現主教圣安布羅斯的“默念”行為與眾不同的。當時，大多數人都大聲朗讀。

當（奧古斯丁）朗讀時，他的眼睛掃視著書頁，他的心在尋找其中的含義，但他的聲音是沉默的，他的舌頭是靜止的。任何人都可以自由地接近他，而客人來訪也通常不會事先通知，因此，當我們去拜訪他時，經常會發現他就這樣靜靜地讀書，因為他從不大聲朗讀。

如今，每個人都認為默念是理所當然的。我們甚至很難想象，默念是怎樣被發明出來的。以前，只為眼睛閱讀的想法是陌生的。

在我們的現代，還有哪些類似的發明是可能的？這些都是我們大多數人當前是無法想象的。

在未來的章節中，我們將看到使用 ZKP 的現有和即將出現的此類發明的模樣。

我把這篇文章寫得比平時長，只是因為我沒有時間把它縮短， 來自 布萊斯-帕斯卡

壓縮（compress）是指 “把東西壓縮到更小的空間”

同樣，簡潔（succinctness）的定義是 “用幾個詞清楚地表達某事的行為”

具有壓縮特性的 ZKP 意味著，我們可以用非常簡短的語句來證明某事為真。例如，某個計算的所有步驟都已正確執行。這在某些資源需求量大、價格昂貴的情況下最為實用。以太坊區塊鏈就是如此，但在其他情況下，這也是一個非常有用的特性。更難能可貴的是，無論我們要證明的事情有多復雜，這個證明的大小都是一樣的！

我們所說的 "證明 "和 "證明的大小 "是什么意思？這些都是數學上的精確概念，其中有很多細微差別。在以后的章節中，我們將結合 ZKP 深入探討證明的概念。現在，我們可以把它看作是一個我們知道是真的，或者可以通過某種方式驗證是真實的簡短陳述。

在典型的偵探小說（如福爾摩斯探案集）中，偵探要收集證據，直到能夠證明兇手犯下了謀殺罪。然后，他們會在最后的大結局中證明他們是如何知道這一點的。我們可以把最后這句話看作證據。

更正式地說，我們將這一屬性稱為*簡潔性（*succinctness*）* 。無論我們要證明什么，證明的大小都是一樣的。就公共區塊鏈而言，這也與可擴展性的概念有關。對于以太坊這樣的公共區塊鏈來說，區塊空間有限且昂貴，ZKP 可以讓交易更便宜、更快速。如何做到這一點？我們創建一個證明，證明某些交易已經發生，并將這個微小的證明放在鏈上，而不是讓所有交易占用區塊鏈的空間。有了 ZKP，這可以變得非常安全。

簡潔性是一種通用屬性，與 "區塊鏈"無關 -- 只是出于多種原因，它們恰好非常適合。一般來說，簡短地證明某事屬實是非常有用的。有幾種方法可以說明原因。

一種方法是考慮*交易成本*。一般來說，交易成本越低，創造的價值和財富就越多。如果需要驗證的事情減少了，或者驗證變得更容易了，那么我們就可以更自由、更輕松地做事。

有時，當我們填寫表格時，會被要求寫兩次電子郵件地址，以確認是否正確。這樣做的目的是防止人為錯誤，使數據轉賬更加穩健。還有像校驗和這樣的東西，在你的 UPS 包裹代碼、信用卡號或書籍的 ISBN 代碼中多加一個數字，就可以簡單地檢查所有數字是否正確。顯然，所有這些都不是為了防止惡意使用，而只是為了防止無意的錯誤。

數據：自朱嘯虎、李寧、倍輕松等購入BAYC以來，地板價跌去至少50%:8月22日消息，朱嘯虎大概在4月底5月初購買了無聊猿猴NFT（#9279），幾乎同時，李寧、倍輕松等中國企業購入無聊猿猴，并成功借勢營銷。Dune數據顯示，當時BAYC的地板價幾乎是歷史最高，大概在125-150E之間。當前，BAYC的地板價大概在61ETTH，這意味著，彼時投資BAYC的朱嘯虎，虧損至少達到了50%。推特大V“Bitcoin女博士”則稱，朱嘯虎購入BAYC的價格在50萬美元，但目前市場價大概在10萬美元。[2022/8/22 12:39:08]

在計算機文件系統中，哈希通常用于確保文件的完整性。如果文件的一小部分發生損壞，哈希值就會完全改變。由于哈希值簡潔明了（例如一個 64 個字符的字符串），即使底層文件非常龐大，也很容易保存和檢查。在此案例中，哈希函數能以安全的方式確保完整性。如果我們只通過保留文件的副本來檢查文件的完整性，那就太不切實際了。大文件、小文件都無所謂，哈希值的大小保持不變。哈希值的簡潔性使得這種應用成為可能。

讓我們從壓縮、簡潔和證明中抽離出來。我們將繞道知識、精神開銷和信任。然后，我們將在本節末尾將其與 ZKP 聯系起來。

在日常生活中，你知道什么是真的，為什么？如果你每天都看到太陽升起，那么你很可能會期待它明天再次升起。在現代社會，我們在很大程度上可以免受自然界惡劣環境的影響，但另一方面，我們也有很多其他更現代的擔憂。其中許多都與我們日常打交道的各種機構有關。

如果你每天都能從銀行提取現金，你是否希望第二天還能再次提取？大多數人可能會說是的，但并不是每個人都能一直這樣做。這取決于很多因素：銀行是否值得信賴，你是否生活在一個安全的司法管轄區，最近世界經濟是否發生了重大事件，你的個人情況如何等等。所有這些因素加在一起構成了一些數據判斷點，你可以據此做出判斷。

這顯然是一個很小的例子，但生活中充滿了這樣的交互。所有這些都可以看作是一種精神開銷。這在多大程度上會引起關注，取決于你的個人情況和日常交易的復雜程度。例如，企業在與另一方簽訂合約時可能會更多地考慮這些因素。

我們建立了一些機制和規則來應對這種不確定性，比如使用聲譽服務、獨立審計、罰款以阻止不良行為、尋求一些可信機構的認證等。所有這些措施基本上都是膠帶，試圖找到問題的關鍵。某些東西是否如其所言？它是否遵循我們制定的規則？它是否值得信賴和可用？

當你要與多個機構、轄區、公司和人員打交道時，所有這些精神負擔都會變得更加沉重。你可能會受到連帶影響，比如你的銀行倒閉，你無法支付員工工資，從而導致你的企業無法為客戶提供服務。需要更多的控制措施。需要更多的停頓來考慮事情是否正確，以及哪些地方會出錯。

我引用一段話來結束本節：

文明的進步是通過增加我們不假思索就能完成的操作數量來實現的。來自 阿爾弗雷德-諾斯-懷特海

例如，當你點燃爐子做晚飯時，你甚至不用考慮生火的問題。這與拾柴、保持干燥、生火、持續生火這一非常耗時的過程截然不同。在數學方面，如果沒有微積分，我們就無法登上月球。

有了 ZKP 和簡潔的證明，我們就能為不透明的系統引入更多確定性和清晰度。當我們考慮組合ZKP 時，這一點變得更加強大。即以某種方式將多個證明合二為一，如聚合或遞歸。

所有這一切都假定我們可以將上面提到的一些機制或規則（通常是混亂和不一致的）轉化為 ZKP 可以理解的形式。我們如何才能做到這一點呢？

回想一下，ZKP 允許我們以通用方式證明任意語句。為什么這很重要？

現有的類似工具和 ZKP 之間的區別就像計算器和計算機之間的區別。一個是用于非常特殊的任務，而另一個則是通用的。這就是計算器和現代計算機之間的區別：

回顧我們上面舉過的具體例子，可以更具體地說明隱私和簡潔性。密碼是允許你登錄某些服務的隱私信息。對于某些輸入數據（如文件）的哈希值來說，它為我們提供了一個簡潔的東西來檢查相等性。

我們可以將哈希函數形象化如下：

我們在一些已知輸入數據上應用特定的哈希函數，如 SHA256 。例如，使用句子 敏捷的棕狐貍會跳過懶惰的狗（不帶引號）作為輸入，并應用 SHA256 哈希函數，結果是哈希值d7a8fbb307d7809469ca9abcb0082e4f8d5651e46d3cdb762d02d0bf37c9e592。在句末添加一個.，就會得到完全不同的哈希值：敏捷的棕狐貍會跳過懶惰的狗.散列值為 ef537f25c895bfa782526529a9b63d97aa631564d5d789c2b765448c8635fb6c。

盡管句子只改變了一點點，但得到的哈希值卻大相徑庭。安全的哈希函數很難被 "破解"，而且具有一些很好的特性。例如，如果掌握了哈希值，就無法創建新的初始輸入。此外，你也無法輕易構造出一個散列為特定、預定散列值的信息。這些哈希函數被稱為*加密哈希函數*。

我們上面使用的 SHA256 哈希函數是一種特定的加密哈希函數，它的安全需要大量時間和許多人的努力。哈希值本身并不能證明什么。它只有在與其他東西（如直接訪問信息或文件）進行比較時才有意義。

YFI核心開發者：ShibaSwap目前是最小可行的版本，所有流動性都可以通過一個地址輕松竊取:yearn.finance（YFI）核心開發者banteg表示，ShibaSwap目前是最小可行的版本，所有流動性都可以通過一個地址輕松竊取，并質疑為什么人們在其中投入了超過1.2億美元？[2021/7/6 0:31:23]

非正式地講，我們可以把哈希函數看作是證明某些特定信息對應于特定哈希值的證據。我們只能用原始信息來驗證這一點。有時，人們會用哈希函數來證明自己寫了什么并進行預測--他們寫道："2040 年 4 月 1 日，外星人將降落在倫敦大本鐘頂端，彩票號碼 25742069 將中大獎。"然后提前公開發布這條信息的哈希值，比如在 Twitter 上。當事實證明他們是對的時候，他們就可以公開原始信息，讓人們相信他們確實預測了未來，是下一個諾斯特拉達穆斯。

相比之下，我們可以將 ZKP 形象化如下：

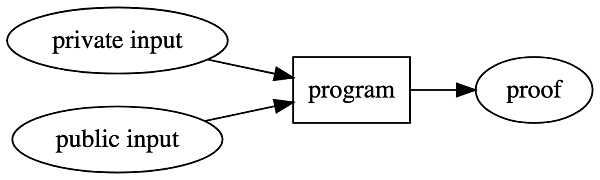
與上面的哈希函數不同，ZKP 有幾個很大的不同點：

我們有多個隱私和公共輸入，而不是只有一個（公共）輸入

我們可以使用任何程序，而不僅僅是加密哈希函數

我們能生成可驗證及自足（self-contained）證明

在上面的哈希函數示例中，我們需要公共輸入，以便驗證信息是否與散列一致。

對于 ZKP，我們也可以使用隱私輸入。隱私輸入是指只有你能看到的輸入。也就是說，你不需要把它透露給任何人，就能生成證明。

例如，在本文開頭的 "沃爾多在哪里"案例中，公共輸入是 "沃爾多在哪里" 的圖片。隱私輸入則是 Waldo 的實際位置。我可以證明我知道沃爾多在哪里，而無需向你透露隱私輸入，即沃爾多的位置。

同樣，如果我有一個數獨謎題（一種流行的邏輯謎題），我可以向你證明我知道謎題的解法，而不向你透露解法。在此案例中，公共輸入是初始謎題，隱私輸入是謎題的解答。

你可能已經注意到，"沃爾多在哪里" 和解數獨謎題是兩個完全不同的問題。然而，我們可以編寫一個簡單的程序來表達這兩個問題的工作原理，并使用 ZKP 進行證明。這是因為這個特殊程序中的邏輯是通用的，可以計算計算機所能計算的任何東西。

我們把原本屬于密碼學或數學的問題--定義加密哈希函數并使其安全--變成了編程問題。要想知道這為什么如此強大，請看下面的一些例子。

我們現在可以證明，我們知道產生某個哈希值的隱私數據。這就意味著，你可以在不泄露信息本身的情況下，證明你掌握了某條信息，比如一份重要文件。

為了更好地理解通用計算的強大功能，讓我們來詳細了解一下群簽名（group signature）。群簽名是一群人共同簽署一份文件的方式，但不會暴露他們的身份。例如，《聯邦黨人文集》就是由代表多個個人的化名 Publius 簽署的。就像 SHA256 哈希函數一樣，有一種方法可以用密碼學和數學來表達群簽名。這非常了不起，需要大量的密碼工程技術才能開發出來。但有了通用 ZKP，任何人都可以用幾十行 Circom（一種 ZKP 編程語言）代碼來表達同樣的內容。

由于其通用性，我們可以很容易地進行特別構造。例如，你可能有一張身份證，上面有你的全名、地址和其他個人信息。要參加某個活動，你可能需要年滿 18 歲并持有有效門票。你可能不希望隨便一個人或在線系統看到你的地址，或冒著身份證被盜的風險。有了 ZKP，你就可以證明這一點：

你持有有效身份證件

該身份證在過去 5 年內由認可機構簽發

身份證最近未被吊銷或報失

年滿 18 周歲

你已購買有效的活動門票

門票之前未被使用過

除上述情況外，不透露你的任何其他信息。

有了 ZKP，我們現在就有了一個好的工具，可以讓人們以各種方式進行協調，尤其是在需要隱私和簡潔的系統中。我們將在應用部分看到更多的例子。

很多時候，你的想象力才是你所能表達的極限。

為什么現在開始流行 ZKP？這既有技術原因，也有社會原因。

從技術上講，ZKP 相當新。從數學上講，它們只存在了幾十年。與計算本身類似，即使在理論上，它也需要一段時間才能變得高性能和實用。

在此之后，必須有人將這些論文和密碼協議轉化為實用的東西。第一個值得注意的例子是 2016 年的隱私保護加密貨幣 Zcash。它最初是由密碼朋克和研究人員撰寫的一篇論文)。第一個版本是將研究和工程應用于最終產品和系統的一項令人印象深刻的壯舉。雖然該系統存在許多問題，而且遠非最佳，但它是在現實世界中使用 ZKP 的第一個真正實用的例子。這向人們表明，在現實世界中使用 ZKP 是可能的，也是切實可行的。這導致了 ZKP 研究和工程工作的爆炸式增長，尤其是在最近幾年。

以太坊和 Zcash（一種保護隱私的加密貨幣）等公共區塊鏈在其中發揮了重要作用。區塊鏈最擅長的是抗審查和透明度。這是以缺乏隱私和可擴展性為代價的，而這正是 ZKP 所擅長的。從這個意義上說，它們是天然的契合點。再加上區塊鏈社區對高級加密技術的需求，難怪很多創新都發生在區塊鏈和 ZKP 的交叉點上。由于許多資本雄厚的區塊鏈項目，這也讓傳統上學術性較強的研究和工程領域有了更多投資。

幣情觀察室 | 一招搞定交易心理管理 輕松玩轉合約:4月8日14:00，金色盤面邀請行情大V梭哈學院做客金色財經《幣情觀察室》直播間，將分享《一招搞定交易心理管理 輕松玩轉合約》，敬請關注，掃描下圖二維碼即可觀看直播！[2020/4/8]

考慮到所涉及的復雜性，包括應用數學、密碼學、關于特定 ZKP 系統的論文、新型證明系統的實施、工具以及涉及其他復雜領域的應用，事情發展得非常快。每年，甚至每個月，都會有新的研究論文，其中包括新技術、改進的工具和應用。新研究成果與實施和應用之間的反饋環越來越緊密。雖然難度依然很大，但入門卻越來越容易。隨著工具的改進，開發人員需要了解 ZKP 背后的數學知識也越來越少。

就 ZKP 的性能而言，摩爾定律的形式正在發生。摩爾定律是指晶體管的數量大約每兩年翻一番。這就是計算機革命的起因。在 ZKPs 中，幾年前還只是白日夢、被視為完全不切實際的項目，現在已經開始實施，比如 zkVM 和 zkML。根據經驗，在 ZKP 領域，每隔一年左右就會有一個數量級的進步。這是因為它是一項新技術，可以在堆棧的多個層面（從我們編寫的程序到我們使用的系統，再到硬件本身）進行積極優化。我們沒有理由相信這種趨勢會很快停止。

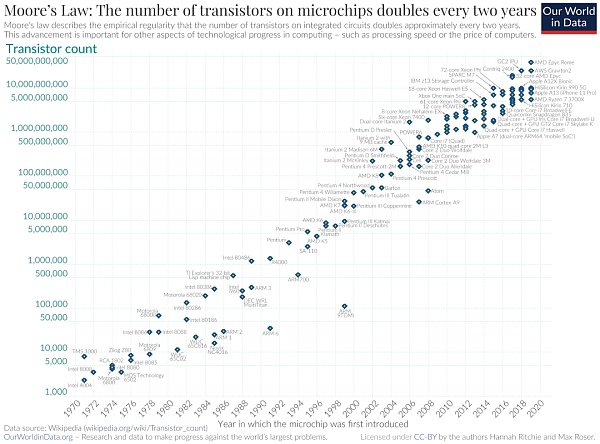
本節從高層次解釋了零知識證明的工作原理*。

本節從高層次概述了零知識證明的工作原理。其中不包括任何數學或代碼。

我們首先介紹一些術語。會有一些新的術語需要學習，但隨著學習的深入，你會慢慢掌握的。

協議（Protocol）：解釋應遵循的正確行為的規則體系

證明（Proof）：確定陳述真實性的論據

證明者（Prover）：證明或演示某事的人

驗證者（Verifier）：保證陳述正確的人

隱私輸入（Private input）：只有證明者能看到的輸入，通常稱為見證（witness）

公共輸入（Public input）：證明者和驗證者都能看到的輸入，通常稱為實例（instance）。

雖然學習該領域的術語很有幫助，但一些比喻也有助于更好地理解其中的含義。我們將陸續介紹更多術語。

協議無處不在，可以是隱性的，也可以是顯性的。在國際象棋游戲中，約定俗成的規則是兩位棋手輪流按照游戲規則走一步棋，直到游戲結束，其中一人獲勝，或者雙方和棋。從理論上講，下一步棋所需的時間并不重要，但在實際操作中，我們會盡量減少互動雙方之間的通信成本。因此，我們可以將其視為一盤真正的快棋。

我們可以把夏洛克-福爾摩斯想象成證明者，在他的最后陳述中，他提出了一系列優雅的論據，即證明（proof），證明某人是兇手。然后，這必須由驗證者（例如法官或陪審團）驗證為真，排除合理懷疑。證明者指的是一個實體，這里是福爾摩斯，他提出證明，然后必須進行驗證。因為證明是自足的（self-contained），所以任何人都可以成為驗證者，包括作為讀者的你，你必須相信所提供的推理，使故事可信。

隱私輸入是一些只有福爾摩斯知道的知識，例如有人在他耳邊說的一些秘密信息。這通常被混淆地稱為見證（witness），大概是因為法庭上的證人擁有一些隱私信息，而這些信息會被添加到證據堆中。而在 ZKP ，這些隱私信息不會與驗證者共享，在這個例子中也不會與法官和陪審團共享。

ZKP 在證明者（Prover）和驗證者（Verifier）之間建立了一個協議（Protocol）。如果證明者和驗證者不需要像下棋或跳舞那樣直接互動或交流，那么這個協議就是非交互式的。取而代之的是，證明者提出一個獨立的證明，并在稍后的某個時刻得到驗證。大多數 ZKP 一開始都是交互式的--即需要多次來回--然后我們使用一些數學技巧使其成為非交互式。你可以把 "非交互式" 想象成兩個棋手，他們在說了幾句話之后，就知道了對方要走的每一步棋，所以他們甚至都不用開始下棋，因為他們已經知道了棋局的結局。

ZKP 有很多種。我們經常談論 zk-SNARKs，它代表零知識簡潔非交互式知識論證（Zero Knowledge Succinct Non-Interactive ARguments of Knowledge）。零知識和簡潔分別對應于上述的隱私和壓縮。提到了非交互式。"知識論據"與證明基本上是一回事。zk-SNARKs 也有許多不同的類型。

一個好的思維模型是把 ZKP 想象成一個動物園。那里有很多動物，我們可以用不同的方式對它們進行分類：這些動物有四條腿，這些動物有條紋，鮑勃去年帶來的動物，等等。有些類別比其他類別更有用。事實上，有些系統甚至沒有 "零知識"（Zero Knowledge）！這些系統通常只被稱為 SNARK。作為一個社區，我們通常稱這種不同動物的動物園為 ZK，即使有許多系統實際上并不使用零知識屬性。

回到我們的協議，我們有一個證明者和驗證者。證明者使用證明者密鑰（prover key,）、隱私輸入和公共輸入創建一個證明。驗證者使用驗證密鑰（_verification key_ ）和公共輸入驗證證明，并輸出真或假。

我們有了兩個新東西：證明者密鑰和驗證者密鑰。這就是證明者和驗證者施展魔法的地方。你可以把它們想象成一把普通的鑰匙，讓你進入某個地方并做某些事情，也可以把它們想象成一根魔法棒，讓你做某些事情。我們從一個叫做setup的特殊儀式中獲得這些密鑰，這是一個初始準備階段，本文不再詳述。

華爾街比特幣公牛Tom Lee認為比特幣在2018年將輕松翻倍 甚至將翻三倍:華爾街最大的比特幣公牛之一，Fundstrat Global Advisors聯合創始人兼研究部主管Tom Lee在接受CNBC的采訪中表示，他認為比特幣1028年可以輕松翻倍，甚至翻三倍。他預計到2018年中期，比特幣將漲至兩萬美元。如果成功在上半年漲至兩萬美元，預計到2018年下半年比特幣漲勢將更加明顯。Tom Lee仍然建議投資者買入/持有比特幣。[2018/1/11]

請注意，只有證明者才能訪問隱私輸入。證明者如何使用證明者密鑰、隱私輸入和公共輸入將其轉化為證明呢？

回想一下之前的 ZKP 插圖：

我們有一個特殊的程序（正式名稱為電路 - circuit），可以編碼用戶關心的邏輯。例如，證明他們知道得出某個哈希值的數據。與普通的計算機程序不同，這個程序是由約束（constraints）組成的。我們要證明的是，所有約束條件都與隱私和公共輸入保持一致。

最后，驗證器將這個簡短的證明與驗證密鑰、公共輸入和包含所有約束條件的特殊程序結合起來，并在排除合理懷疑的情況下確信證明是正確的，然后輸出 "true"。如果不正確，則輸出 "假"。

以上觀點略顯簡單，但卻抓住了事情的本質。

構成上述特殊程序的約束條件是什么？約束是一種限制或制約。例如，"1 到 9 之間的數字 "就是一個約束。數字 7 滿足這個約束，而數字 11 不滿足。如何將程序寫成一組約束？這本身就是一門藝術，讓我們先看一個簡單的例子：數獨

在數獨游戲中，我們的目標是在棋盤上找到滿足某些約束條件的解。每一行都必須包含數字 1 到 9，但只能包含一次。每列和每個 3x3 子方格也是如此。我們會得到一些初始的起始位置，然后我們的任務就是以滿足所有這些約束條件的方式填入其余的位置。最棘手的部分是找到同時滿足所有限制條件的數字。

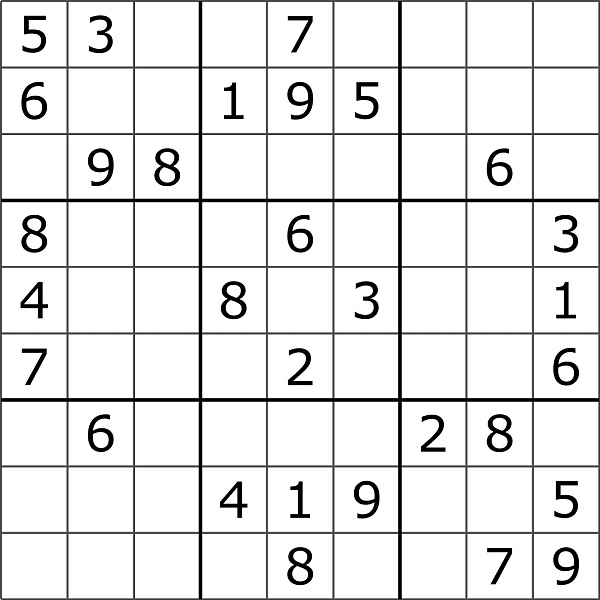
通過 ZKP，證明者可以構建一個證明，證明他們知道某個謎題的解。在此案例中，證明包括使用一些公共輸入（初始棋盤位置）和一些隱私輸入（謎題的解法）以及一個電路。電路由表達謎題的所有約束條件組成。

之所以稱其為電路，是因為這些約束條件彼此相關，我們將這些約束條件連接起來，有點像電路。在此案例中，電路處理的不是電流，而是數值。例如，我們不能把任何類似 "香蕉 "的值添加到我們的行約束中，它必須是一個數字，而且這個數字必須介于 1 和 9 之間，以此類推。

驗證者擁有相同的電路和公共輸入，可以驗證證明者發送給他們的證明。如果證明是有效的，驗證者就會確信證明者已經找到了該謎題的解。

事實證明，很多問題都可以用一組約束來表示。事實上，我們能用計算機解決的任何問題都可以用一組約束來表示。

讓我們把學到的有關 ZKP 各部分的知識應用到上面的數獨例子中。

在數獨游戲中，我們的特殊程序電路需要兩個輸入：

作為公共輸入的數獨謎題

數獨謎題的解作為隱私輸入

電路由一系列約束條件組成。所有這些約束條件都必須為真。這些約束條件是這樣的

謎題和謎底中的所有數字必須介于 1 和 9 之間

解決方案必須是謎題中所有位置均放置了數字

所有行中必須包含從 1 到 9 的數字，且每個數字只出現一次

所有列中必須包含從 1 到 9 的數字，且每個數字只出現一次

所有子方格中必須包含從 1 到 9 的數字，且每個數字只出現一次

如果一道謎題及其解法的所有這些限制條件都為真，那么我們就知道它是一個有效的解法。

證明者 Peggy 使用她的神奇證明者密鑰、謎題和解法，將其與特殊程序結合，創建一個證明。證明非常簡短，不到 1000 個字符。證明是自足的（self-contained），驗證者可以通過它獲得驗證證明所需的所有信息。你可以把它想象成一個魔法咒語，它能實現你的愿望，而你無需了解其中的細節。

下面是 19 世紀一位威爾士醫生寫的一本魔法書中的咒語：

下面是一個由 Circom/snarkjs 庫生成的零知識證明示例：

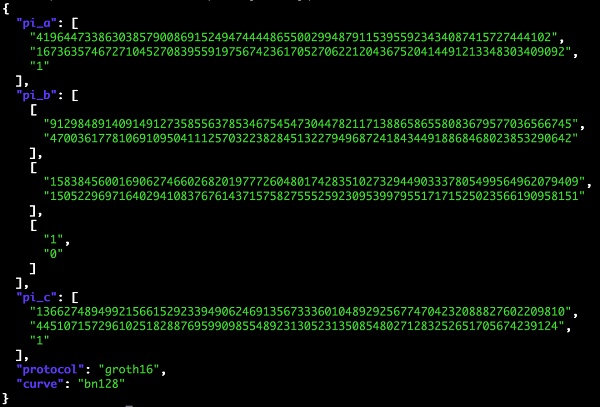
在此案例中，魔法確實起作用了。

驗證者 Victor 使用他的驗證密鑰、原始謎題輸入，驗證 Peggy 發送的證明是否正確。如果正確，則輸出 "真"；如果不正確，則輸出 "假"。咒語要么有效，要么無效。這樣，Victor 就確信 Peggy 知道那個特定謎題的解法，而實際上并沒有看到解法。就是這樣。

我們說 ZKP 具有某些技術特性：

完備性（Completeness） -- 如果聲明為真，那么驗證者將被證明所說服

可靠性（Soundness） -- 如果語句為假，驗證者將不會被證明所說服

零知識（Zero Knowledge） -- 如果語句為真，除了它為真這一事實外，不會透露任何其他信息

此外，對于 zk-SNARKs 來說，證明是簡潔的，這意味著它基本上不會隨著程序變得越來越復雜而變大。

在實際的 ZKP 中，我們還關心許多其他特性：

系統做了哪些數學假設？

安全性如何？

是否需要可信的設置？

生成證明有多難？時間和其他資源

驗證證明有多難？時間和其他資源

ZKP 系統是否允許將多個證明聚合在一起？

是否有可供程序員使用的 ZKP 系統庫？

用于編寫特定 ZKP 系統程序的語言的表現力如何？

正如你所看到的，ZKP 有很多考慮因素和不同的變體。不過不用擔心，要點基本上都是一樣的，而且根據你的興趣所在，你可以對其中涉及的許多技術細節一無所知。回到動物園的比喻，就像對待動物一樣，你可能并不想成為一名生物學家。相反，你可能想和一些動物打交道，或者你只是想養一只寵物，甚至只是想摸摸你朋友的狗。

本節將舉例說明 ZK 當前和未來的應用

ZKP 有許多應用。一般來說，我們仍處于早期階段。很多焦點仍然集中在底層協議和基礎設施，以及區塊鏈的特定應用上。要想更好地理解區塊鏈的具體例子，最好對公共區塊鏈的工作原理及其面臨的挑戰有一定的了解。不過，這并不是必要條件。在本節中，我們將介紹一些更有趣的應用。我們將先看看現在已經上線的應用，然后再看看即將上線的應用。

未來已來。只是分布還不均勻。來自 威廉-吉布森

電子現金：要在網上建立類似現金的支付系統，就必須像實物現金一樣具有可替代性和私密性。可替代性是指一種商品可被另一種相同商品替代的特性。也就是說，你的錢和我的錢沒有區別，它們都是同樣有效的支付形式。與比特幣或以太坊不同，我們可以使用 ZK 使交易歷史隱私化。這樣，你的交易歷史就不會被公開，從而確保電子現金的可替代性。目前，Zcash 等系統以及Tornado Cash等相關系統都采用了這種方式。

匿名信號 ：通常，我們可能需要在不暴露身份的情況下證明自己隸屬于一個具有某些特征的群體。其中一個例子是證明自己是某個群體的一員；另一個例子是投票。這意味著你不會把自己的身份與敏感的行為聯系在一起，比如你投票給哪個政黨，或者泄露其他不必要的信息。目前，Semaphore等系統中就有類似的機制，而且還有很多變種。

ZK Rollup：允許更多、更便宜、更快速的交易。以太坊區塊鏈空間有限，價格昂貴，需求量大。我們使用所謂的第二層（L2） Rollup ，與主區塊鏈（L1）分開進行交易。一旦有一定數量的交易進入 L2 層，它就會將其 "打包"到 L1 層。ZKP 在這方面非常有用，因為我們可以（i）證明交易執行正確，（ii）創建一個簡潔的證明，只占用 L1 上的少量空間。這就使得交易對用戶來說更便宜、更快捷，同時具有近乎同等的安全性。由于證明整個以太坊虛擬機（EVM）執行的復雜性，許多 ZK Rollup 解決方案從關注簡單商資產的交換開始。目前在 Loopring、zkSync Lite、dYdX 和 Starknet 等系統中都有應用。

ZK-EVM: 與 ZK Rollup 類似，但具有通用性，因為可以執行任何類型的交易或程序。以太坊有一個 EVM，它就像一臺全球共享的通用計算機（任何人都可以寫入）。通過使用 ZKP 編寫該機器的邏輯，我們可以證明在以太坊上編寫的任何程序的正確執行，并構建一個簡潔的證明，證明該程序被正確執行。這有多種使用場景，但最直接的使用場景是擴展和允許更便宜、更快速的交易。目前已在 Polygon zkEVM、zkSync Era 等系統中使用，其他一些ZKEVM系統也即將使用 。

**ZK-VM: **部分原因是針對像 EVM 這樣的 "SNARK 不友好" 平臺的復雜性，許多項目選擇做一個獨立于以太坊的新區塊鏈。這意味著他們可以首先優化虛擬機，以便更好地與 ZK 協同工作。根據具體系統的不同，這可以實現區塊鏈狀態的隱私和簡潔驗證。Mina 已經上線，Aleo 等系統正在積極開發中。

對 snark 不友好的平臺或函數指的是大多數現代計算機原語都是為特定的計算機體系結構設計的。這種架構與編寫約束時的架構非常不同。例如，SHA256 哈希函數就是一個典型的 snark 不友好哈希。有些人創建了 SNARK 或 zk 友好的函數，例如 Poseidon 哈希函數，專門設計用于 zkp。這些在 zkp 中更容易實現，并且效率可以提高 100 倍或更多

黑暗森林: 黑暗森林是一款不完全信息實時策略游戲。基于 ZK 的不完全信息游戲有一個 "加密戰爭迷霧"，玩家只能看到世界的一部分，這是 ZK 強制實施的。與《星際爭霸》等傳統游戲相比，即使是中心化服務器也無法獲得所有信息。由于其程序化的特性，這使得新穎的游戲方式成為可能。

ZK 跨鏈橋 - 跨鏈橋允許你在不同的區塊鏈和系統之間移動資產。這些跨鏈橋很難保證安全，而且經常被黑客攻擊。有了 ZK，我們可以更安全、更快速地連接資產，而無需依賴可信的第三方或容易出錯的方法。目前，zkBridge 已投入使用，Succinct Labs 等項目也正在進行相關工作。

隱私身份 : 隨著越來越多的獨立系統需要并托管我們的在線身份，個人最好能夠擁有、整合并保持這些去中心化的在線身份的私密性。目前，Sismo 等項目已經實現了這一點，其他項目也在開發類似的系統。

以上只是幾個例子，絕不完整。我們還沒有談到隱私不可抵賴聲譽、導出 Web2 聲譽、抗 sybil 拒絕服務保護、抗脅迫證明、復制證明、匿名空投、分離度證明等。

ZK-EVM（以太坊等價性）：ZK-EVM 有不同的類型，實現起來更具挑戰性的是那些完全等同于以太坊的 ZK-EVM。其他 ZK-EVM 會采取一些捷徑，讓生成證明變得更容易。完全等同于以太坊的 ZK-EVM 與當前的以太坊系統沒有區別。這意味著我們可以用簡潔的證明來證明存在的每一個區塊的正確執行。你可以用手機驗證整個鏈的完整性，完全依靠數學，而無需信任第三方或使用昂貴的機器。目前 ZK-EVM 社區團隊正在開發中。

通用可證明計算：世界上大多數計算都不在 EVM 中進行，而是在其他系統中進行。基于 WASM 和 LLVM 的程序非常常見。我們可以利用 ZK-EVM 中的相同方法，進行通用的隱私可證明計算。例如，我們可以在不透露任何其他信息的情況下證明數據庫包含特定記錄。目前，許多不同的團隊，例如 Delphinus Labs、RISC Zero、Orochi Network 和 nil.foundation，都在研究這一技術。

ZK 機器學習（ZK ML）：我們可以在鏈外私下證明某些計算是正確完成的，然后公布計算正確的證明。這意味著，我們可以使用隱私數據來訓練更好的模型，而不會泄露這些數據。例如，敏感文件、語音，甚至 DNA 等用于發現健康問題的數據。這既提高了可擴展性，又保護了用戶隱私。目前已有一些概念驗證（PoC），如 MNIST（機器學習中用于識別手寫數字的常用測試），人們正在研究更復雜的東西，如 ZKP 內部的神經網絡。

照片真實性：證明照片和視頻等內容的出處，包括標準的后期處理編輯。也就是說，證明照片是在特定時間和地點拍攝的，并且只進行了基本的大小調整、裁剪和灰度使用（美聯社認可的操作列表）。已經有一些概念證明工作。

合規性：證明隱私交易符合某些規定，或某項資產不在特定的黑名單上。在不泄露資產的情況下證明交易所有償付能力。Espresso Labs 等系統已經做了一些工作，有些系統已經有了簡單的版本。

隱藏意圖 ：公共區塊鏈的用戶有他們想要實現的特定目標，這些目標可以用意圖來表達。例如，用戶可能想用一種代幣兌換另一種代幣。用戶可以將自己的意圖告訴其他用戶，并與合適的對手方進行匹配。最好能對這些意圖進行屏蔽（隱藏 "誰 "而不是 "什么"，類似于 Zcash 中的屏蔽交易）或完全保密。目前，Anoma 正在從屏蔽意向匹配開始研究。要使意圖匹配完全保密，可能需要在密碼學方面取得突破性進展，這與本節最后一個例子類似。

自主世界：這是《黑暗森林》等作品的延續。世界可以是物理的，也可以是概念的，如納尼亞世界、基督教、美元世界、比特幣或英聯邦法律。根據這些世界的運行情況，如果任何人都可以在不破壞其客觀性的情況下改變規則，那么這些世界就可以是自主的。目前，0xPARC 基金會正在游戲和創建這些世界的背景下進行探索。

數據真實性證明：從網絡應用程序中導出數據，并以非公開方式證明相關事實。使用 TLS 協議，這意味著它可以在任何現代網站上運行。目前由 TLSNotary 負責開發。

核裁軍：允許檢查核設施的人在不檢查任何敏感的內部工作原理的情況下，確認某個物體是否是核武器。已有物理模擬工作的論文。

和談與高風險談判：在談判中，人們通常會有一些硬性限制，他們不希望向對方透露這些限制，以削弱自己的談判能力。通過對這些限制進行明確編碼，雙方可以就一些高度復雜的領域進行談判，并在不透露其精確參數和限制細節的情況下達成協議。這樣，互不信任的雙方也能達成某種協議。這可能需要在多方計算（MPC）方面取得一些突破，它允許我們在共享秘密的基礎上進行計算。

同樣，這里并沒有提到人們正在研究或思考的所有類型的問題。未來肯定還會有更多的東西。正如你所看到的，我們可以用 ZK 做很多事情。

你可能會問，為什么這些應用中有很多涉及區塊鏈。上一節 "為什么是現在？"已經部分回答了這個問題。ZK 是一種與以太坊等區塊鏈正交的技術，我們可以不使用區塊鏈，但在很多情況下，它只是一種可以利用的好工具。

同樣，從事這些工作的人群和他們關心的直接問題往往是重疊的。隨著這個領域的成熟，我們可以預見，ZK 應用中的 "區塊鏈 "部分將不再僅僅是一個實施細節，而這在某種程度上已經發生了。再進一步看，"ZK"部分也很可能會消失，它將只是一個碰巧使用 ZKP 的應用程序。

最后，當在線信息和類似的加密技術被開發出來時，它是由軍方和互聯網公司使用和開發的。這不是郵局或某些從事實物安全運輸的公司的創新成果，即使理論上有這種可能性。

在本節的最后，我想引用巴里-懷特哈特（Barry Whitehat）在被問及對 ZK 未來的預測時的一段話作為結束語，他是一位著名的 ZK 研究員，在以太坊基金會的隱私和可擴展性探索（PSE）團隊工作：

"到 2040 年，會有人因為使用零知識證明而獲得諾貝爾和平獎"。

離奇而大膽？當然。結果會是真的嗎？也許不會。但可能嗎？絕對有可能。這是一個耐人尋味的前景。將其視為真實可能的心智模式與立即將其一筆勾銷的心智模式之間有什么區別？要讓這樣的事件成為現實的結果，必須發生什么？

ZKP 是一種全新的、非常有效的工具。限制我們的往往是我們對其潛在應用的想象力。

本節對文章進行了總結，并提出了下一步的計劃

在本文中，我們了解了什么是 ZKP、為什么要關注它們以及它們何時有用。我們還了解了它們的工作原理，以及它們為我們提供了哪些屬性。最后，我們探討了一些應用，包括當前和未來的應用。

我希望這能讓你更好地理解 ZKP 的本質，或許還能讓你產生一些 "啊哈"時刻，并啟發你以新的方式思考問題。也許它還能幫助你在未來追隨 ZKP 的魔力。

在今后的文章中，我們將更深入地探討其中的一些方面，我們還將研究更多技術方面的問題，以便更好地理解 ZKP 的工作原理以及它們的用途。

如果某些具體內容引起了你的興趣，或者你希望在今后的文章中看到某些具體內容，請隨時通過 Twitter 或電子郵件與我聯系。

感謝 Michelle Lai、Chih-Cheng Liang、Jenny Lin、Anna Lindegren 和 Eve Ko 閱讀初稿并提供反饋。

本翻譯由 DeCert.me 協助支持， 來 DeCert 碼一個未來， 支持每一位開發者構建自己的可信履歷。

登鏈社區

個人專欄

閱讀更多

Foresight News

金色財經 Jason.

白話區塊鏈

金色早8點

LD Capital

-R3PO

MarsBit

深潮TechFlow

Tags：ZKPQUO區塊鏈以太坊zkProofQUO價格區塊鏈域名交易平臺以太坊幣最新價格行情新浪

火幣交易所