BSP:一文了解FPGA和GPU加速零知識證明計算的優缺點_FPG價格

零知識證明技術應用越來越廣，隱私證明，計算證明，共識證明等等。在尋找更多更好的應用場景的同時，很多人逐步發現零知識證明證明性能是個瓶頸。Trapdoor Tech 團隊從 2019 年開始深入研究零知識證明技術，并一直探索高效的零知識證明加速方案。GPU 或者 FPGA 是目前市面上比較常見的加速平臺。本文從 MSM 的計算入手，分析 FPGA 和 GPU 加速零知識證明計算的優缺點。

ZKP 是擁有未來廣泛前景的技術。越來越多的應用開始采用零知識證明技術。但 ZKP 算法比較多，各種項目使用不同的 ZKP 算法。同時，ZKP 證明的計算性能比較差。本文詳細分析了 MSM 算法，橢圓曲線點加算法，蒙哥馬利乘法算法等等，并對比了 GPU 和 FPGA 在 BLS 12 _ 381 曲線點加的性能差別。總的來說，在 ZKP 證明計算方面，短期 GPU 優勢比較明顯，Throughput 高，性價比高，具有可編程性等等。FPGA 相對來說，功耗有一定的優勢。長期看，有可能出現適合 ZKP 計算的 FPGA 芯片，也可能為 ZKP 定制的 ASIC 芯片。

ZKP 是個零知識證明技術的統稱（Zero Knowledge Proof）。主要由兩種分類：zk-SNARK 以及 zk-STARK。zk-SNARK 目前常見的算法是 Groth 16 ，PLONK，PLOOKUP，Marlin 和 Halo/Halo 2 。zk-SNARK 算法的迭代主要是沿著兩條方向： 1/ 是否需要 trusted setup 2/ 電路結構的性能。zk-STARK 算法的優勢是毋需 trusted setup，但是驗證計算量是對數線性的。

Bitfinex將于7月11日移除BAT/USDT、ID/USDT、TREEB/USDT、EOS/EUR交易對:6月30日消息，據官方公告，Bitfinex將移除如下4個交易對：BAT/USDT、ID/USDT、TREEB/USDT、EOS/EUR。這些交易對的移除將有助于鞏固和改善Bitfinex的流動性，為客戶帶來更精簡和優化的交易體驗。

這四個交易對將于2023年7月11日上午10:00（UTC時間）停止交易。請注意，相關代幣的其他交易對并未移除，仍可在Bitfinex上交易。請客戶在這些交易對下架之前取消任何未完成訂單，這些訂單屆時將被系統取消。

從2023年7月4日上午10:00（UTC時間）開始，客戶只能減少EOS/EUR的保證金頭寸。所有剩余的保證金訂單將被取消，Bitfinex將在2023年7月11日強制結算所有未平倉保證金頭寸。[2023/6/30 22:09:59]

就 zk-SNARK/zk-STARK 算法的應用來看，不同項目使用的零知識證明算法相對分散。zk-SNARK 算法應用中，因為 PLONK/Halo 2 算法是 universal（無需 trusted setup），應用可能越來越多。

以 PLONK 算法為例，剖析一下 PLONK 證明的計算量。

比特幣全網未確認交易數量為25392筆:金色財經報道，據BTC.com數據顯示，目前比特幣全網未確認交易數量為25392筆，全網算力為321.13 EH/s，24小時交易速率為4.10交易/s，目前全網難度為43.55 T，預測下次難度上調4.71%至45.60 T，距離調整還剩9天11小時。[2023/3/15 13:04:38]

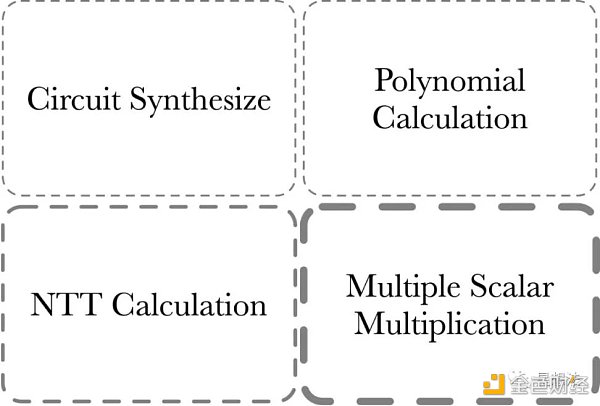
PLONK 證明部分的計算量由四部分組成：

1/ MSM - Multiple Scalar Multiplication。MSM 經常用來計算多項式承諾。

2/ NTT 計算 - 多項式在點值和系數表示之間變換。

3/ Polynomial 計算 - 多項式加減乘除。多項式求值（Evaluation）等等。

4/ Circuit Synthesize - 電路綜合。這部分的計算和電路的規模 / 復雜度有關。

Circuit Synthesize 部分的計算量一般來說判斷和循環邏輯比較多，并行度比較低，更適合 CPU 計算。通常來講，零知識證明加速一般指的是前三部分的計算加速。其中，MSM 的計算量相對來說最大，NTT 次之。

MSM（Multiple Scalar Multiplication）指的是給定一系列的橢圓曲線上的點和標量，計算出這些點加的結果對應的點。

Kraken上的ETH 24小時永續期貨合約交易量達到5年低點:金色財經報道，Glassnode數據顯示，ETH永續期貨合約交易量（24小時）在Kraken上達到5年低點的98,708美元。[2022/10/9 12:49:54]

比如說，給定一個橢圓曲線上的一系列的點：

Given a fixed set of Elliptic curve points from one specified curve:

[G_ 1, G_ 2, G_ 3, ..., G_n]

以及隨機的系數：

and a randomly sampled finite field elements from specified scalar field:

[s_ 1, s_ 2, s_ 3, ..., s_n]

MSM is the calculation to get the Elliptic curve point Q:

Q = \sum_{i= 1 }^{n}s_i*G_i

行業普遍采用 Pippenger 算法對 MSM 計算進行優化。深入看看 Pippenger 算法的過程的示意圖：

美參議員聯名致信OCC署長，呼吁對銀行與加密貨幣互動進行更嚴格的限制:8月11日消息，美國參議員 Elizabeth Warren、Dick Durbin、Sheldon Whitehouse、Bernie Sanders 聯名致信美國貨幣監理署（OCC）署長 Michael Hsu ，要求取消拜登政府從前任政府那里獲得的一系列解釋性指南，呼吁對銀行與加密貨幣互動進行更嚴格的限制。

注：美國前總統特朗普曾任命Brian Brooks領導 OCC，在其任內OCC發布了一系列解釋，基本上給了銀行不受限制的機會來從事某些加密活動，并且仍然存在問題。（The Block）[2022/8/11 12:17:32]

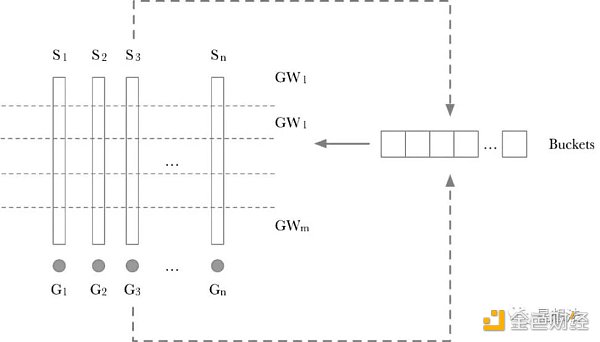
Pippenger 算法的計算過程分成兩步：

1/ Scalar 切分為 Windows。如果 Scalar 是 256 bits，并且一個 Window 是 8 bits，則所有的 Scalar 切分為 256/8 = 32 個 Window。每一層的 Window，采用一個「Buckets」臨時存放中間結果。GW_x 就是一層上的累加結果的點。計算 GW_x 也比較簡單，依次遍歷一層中的每個 Scalar，根據 Scalar 這層的值作為 Index，將對應的 G_x 加到相應的 Buckets 的位上。其實原理也比較簡單，如果兩個點加的系數相同，則先將兩個點相加后再做一次 Scalar 加，而不需要兩個點做兩次 Scalar 加后再累加。

美國6月非農就業人數增加37.2萬人，失業率為3.6%:7月8日消息，美國6月非農就業人數增加37.2萬人，預估為26.8萬人，前值為39萬人。美國6月失業率為3.6%，預期3.6%，前值3.6%。（金十）[2022/7/8 2:01:06]

2/ 每個 Window 計算出來的點，再通過 double-add 的方式進行累加，從而得到最后的結果。

Pippenger 算法也有很多變形優化算法。不管怎么說，MSM 算法的底層計算就是橢圓曲線上的點加。不同的優化算法，對應不同的點加個數。

你可以從這個網站看看具有「short Weierstrass」形式的橢圓曲線上點加的各種算法。

http://www.hyperelliptic.org/EFD/g 1 p/auto-shortw-jacobian-0.html#addition-madd-2007-bl

假設兩個點的 Projective 坐標分別為（x 1, y 1, z 1) 和 （x 2, y 2, z 2) ，則通過如下的計算公式可以計算出點加的結果 (x 3, y 3, z 3)。

詳細給出計算過程的原因是想表明整個計算過程絕大部分是整數運算。整數的位寬取決于橢圓曲線的參數。給出一些常見的橢圓曲線的位寬：

BN 256 - 256 bits

BLS 12 _ 381 - 381 bits

BLS 12 _ 377 - 377 bits

特別注意的是，這些整數運算是在模域上的運算。模加 / 模減相對來說簡單，重點看看模乘的原理和實現。

給定模域上的兩個值：x 和 y。模乘計算指的是 x*y mod p。注意這些整數的位寬是橢圓曲線的位寬。模乘的經典算法是蒙哥馬利乘法（Montgomery Muliplication)。在進行蒙哥馬利乘法之前，被乘數需要轉化為蒙哥馬利表示：

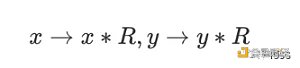
蒙哥馬利乘法計算公式如下：

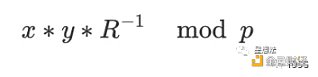
蒙哥馬利乘法實現算法又有很多：CIOS (Coarsely Integrated Operand Scanning)，FIOS（Finely Integrated Operand Scanning），以及 FIPS（Finely Integrated Product Scanning）等等。本文不深入介紹各種算法實現的細節，感興趣的讀者可以自行研究。

為了對比 FPGA 以及 GPU 的本身的性能差別，選擇最基本的算法實現方法：

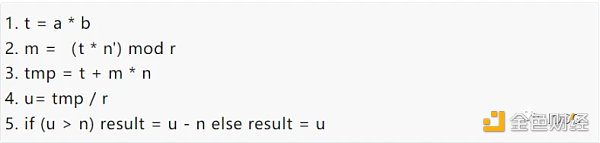
簡單的說，模乘算法可以進一步分成兩種計算：大數乘法和大數加法。理解了 MSM 的計算邏輯的基礎上，可以選擇模乘的性能（Throughput）來對比 FPGA 和 GPU 的性能。

在這樣的 FPGA 設計下，可以估算出整個 VU 9 P 能提供的在 BLS 12 _ 381 橢圓曲線點加 Throughput。一個點加（add_mix 方式）大約需要 12 個模乘。FPGA 的系統時鐘為 450 M。

在同樣的模乘 / 模加算法下，采用同樣的點加算法，Nvidia 3090 的點加 Troughput（考慮到數據傳輸因素）超過 500 M/s。當然，整個計算涉及到多種算法，可能存在某些算法適合 FPGA，有些算法適合 GPU。采用一樣的算法對比的原因，想對比 FPGA 和 GPU 的核心計算能力。

基于上述的結果，總結一下 GPU 和 FPGA 在 ZKP 證明性能方面的比較：

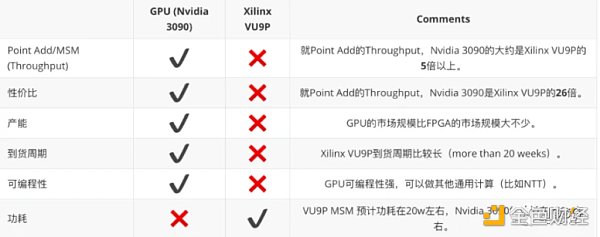
越來越多的應用開始采用零知識證明技術。但 ZKP 算法比較多，各種項目使用不同的 ZKP 算法。從我們的實踐工程經驗來看，FPGA 是個選項，但是目前 GPU 是個性價比高選項。FPGA 偏好確定性計算，有 latency 以及功耗的優勢。GPU 可編程性高，有相對成熟的高性能計算的框架，開發迭代周期短，偏好需要 throughput 場景。

IOSG Ventures

企業專欄

閱讀更多

金色財經

SevenUp DAO

金色圖覽

LK Venture

金色薦讀

區塊律動BlockBeats

Tags：BSPNBSFPGZKPBSP價格nbs幣前景FPG價格ZKP價格

Gateio