金色學院前沿課第六講: 零知識證明:潛力與價值

本課主題：零知識證明:潛力與價值

課程介紹：也許你曾經聽說過ZK Proof或零知識證明。但是，你好像從來沒搞清楚它是什么？在本節課中，你所有關于零知識證明的問題都將得到解答，我們從例子出發，講解什么是零知識證明以及零知識證明如何被用于SK-SNARK和PLONK協議中。

課程大綱：

1. 什么是零知識證明ZKPs

2. 舉例說明零知識工作原理及特征

3. ZKP在區塊鏈中發揮何種優勢

4. 分析零知識證明在未來有何前景

導師簡介：

王澤華

加拿大UBC大學客座教授、博士、博導；加拿大Verilog Solutions Inc.創始人；加拿大英屬哥倫比亞大學客座教授；以太坊基金會合作伙伴。

王澤華博士，Verilog Solution安全審計公司創始人。加拿大UBC大學電子與計算機工程系客座教授，博士生導師。參與創辦的UBC大學區塊鏈研究生項目2021年排名加拿大第一。他在UBC開設的區塊鏈核心課程包括區塊鏈基礎和區塊鏈軟件工程，每年培養上百名Web3行業從業者。王澤華博士2009年畢業于武漢大學軟件工程專業，2016年獲得UBC大學博士學位，其任職首席科學家的RightMesh項目在2018年獲得加拿大總理特魯多表彰。2019年回UBC任教，2021年創辦Verilog Solutions Inc. 區塊鏈安全審計公司，目前是多家公鏈生態和風投基金的官方合作伙伴。

課程內容：

大家好非常感謝金色財經的邀請，今天為大家帶來了零知識證明的潛力與價值系列講座。

1. 什么是零知識證明

首先，什么是零知識證明？零知識證明有的時候指的是零知識證明本身，泛指一切可以不需要泄露任何有用信息即可以證明我知道這些知識的方法。同時零知識證明有的時候也可以用來指代零知識證明實現的算法和協議。這里有必要指出的是零知識證明實質上是一種涉及兩方和更多方的協議及兩方和更多方完成一項任務所需采取的一系列步驟證明者向驗證者證明并使其相信自己知道或擁有某一消息但證明過程不能向驗證者泄露任何關于被證明消息的信息。最后一點，零知識證明也可以用來指代零知識證明過程中交互的消息。雖然擁有知識和信息的一方即證明方不需要告訴被要求相信的一方（即，驗證方）這些信息本身但是驗證方需要和證明方產生交互才能達到信任證明方的目的。這些交互的消息有時候也會被稱為零知識證明。

金色午報｜12月31日午間重要動態一覽:7:00-12:00關鍵詞：以太坊、宮崎駿、Efinity

1.以太坊社區提出新的ETH2.0分片方案；

2.元宇宙商標申請量達1.2萬枚；

3.宮崎駿的十部畫作首次以NFT結合形式發售；

4.NFT公鏈Efinity贏得波卡第6次平行鏈插槽拍賣；

5.Coinbase發布2022年Web和加密經濟的10個預測；

6.EOS網絡Core+藍皮書計劃在1月下旬發布；

7.被標記為第三大比特幣巨鯨地址在12月29日增加120 個BTC；

8.美國SEC任命新的加密貨幣高級顧問；[2021/12/31 8:16:20]

所以我們在說零知識證明的時候，根據語境的不同強調的側重點也不同。有的時候我們說的是零知識證明的算法，有的時候我們說的是零知識證明在驗證過程中交互的消息。但是無論怎樣，我們都需要了解零知識證明是如何工作的，我們需要掌握的是零知識證明是如何可以達到不告知對方有用信息的情況下達到向對方證明我知道這些信息的目的的。

為了講清楚零知識證明我們需要從一個計算機科學里面的基本概念講起這個概念就是P問題和NP問題。P問題指的是在多項式時間內可以解決和驗證的問題，NP問題是指在多項式時間內可以驗證但是目前為止找不到多項式時間內完成的解決方法的問題。現在計算機科學領域普遍認為P問題不等于NP問題。我們比較感興趣的是這種NP問題，也就是說給定一個問題，并且給出這個問題的一個解答，人們很容易在多項式時間內判別這個解答是不是正確的。但是想找到一個正確的解，很難在多項式時間內實現。

這里我們可以想幾個例子，什么樣的問題是我們所感興趣的NP問題呢？比如，分解由兩個很大的質數相乘得到的合數。我們想要分解這樣一個很大的合數需要耗費很多的計算資源，但是給出了其中的一個質因數我們就可以很容易的得到其他一個。而且驗證一個解非常容易，只要將這兩個質數相乘看看是不是等于這樣個比較大的合數就可以了。另外一個NP問題比如說，三色問題。三色問題指的是在一個有點和邊連接的圖中，如何將網絡中的點著色，使得有公共邊的結點顏色互不相同。如果我們知道一個解，我們很容易去驗證它是不是對的，但是找到一個這樣正確的解需要花費很長時間。另外，比如說四色問題，如何給地圖填色使得相鄰的州或者相鄰的國家顏色不同。如果我們知道一個解，我們很容易去驗證它是不是對的，但是找到一個這樣的解需要耗費很長的計算時間。

金色相對論 | 蘭洪明：比特幣已經引起了很多傳統金融玩家的關注:在今日舉行的《危機向左，信仰向右》的比特幣減半特輯直播中，針對“加密貨幣以及加密貨幣行業的項目標的是否能成為傳統資本日常資金配置中的一部分”的問題，啟賦資本蘭洪明表示，比特幣已經引起了很多傳統金融玩家的關注，并且有傳統金融機構已經在大規模布局比特幣，他們玩法還比較特別，一般不在二級市場買的幣，而是直接在礦場買的原生的礦幣（因為他們會考慮合規的問題）。根據我過去一些的經驗，在傳統的二級金融市場通過一般都是通過資產配置的方式，每年有10-15%收益就很不錯，但把比特幣加到投資組合中可以做到超20%年化收益。巴菲特也就是年化20%的收益，不過他非常穩定。專業機構追求的穩定的收益，所以基本上不會追漲殺跌，也不會去預測市場，只是會把BTC所以資產組合中的一部分，不斷的通過動態平衡的方式把錢賺了。更多詳情見原文鏈接。[2020/5/11]

在知道了NP問題的基本概念之后，我們就可以開始梳理零知識證明的脈絡了。首先零知識證明是一套基于數學的程式化的算法，這種程式化的算法可以很容易用計算機幫助我們實現我們的目。我們需要構建一個NP問題，而且這個NP問題的答案就是我們的知識。我們想要證明我們知道這個知識，但是不想告訴別人這個知識究竟是什么。同時，我們也不能直接就把這個NP問題告訴別人，因為如果直接把這個問題告訴別人，就意味著除了告訴別人真正的答案和知識，沒有別的方法證明我知道這個知識，也就無法做到零知識證明了。

那怎么辦呢？我不能告訴你這個NP問題本身，我更不能告訴你這個NP問題的答案。我們需要做的，首先是把我的這個NP問題的解，帶入到我的NP問題當中，并把原來的NP問題轉換成等式的形式。再把這個等式的形式轉化為另一個維度下的另一個NP問題，這個轉化后的新的NP問題會被分解成比較方便驗證的形式。這樣做的目的是，別人可以驗證的是這個新的NP問題，這個新的NP問題是原NP問題將解代入后的一種變化形式。別人知道的是，只有在知道原問題的解的情況下才能完成這種變化，那他就會相信我知道原問題的解了。

分析 | 金色盤面：BTC期貨合約持倉變化:金色盤面綜合分析： 據OKEX數據顯示，目前做多賬戶59%，做空賬戶40%，多頭持倉比例24.04%，空頭持倉比例17.08%，從數據看，多空持倉比例差值再次增大。截至發稿，當周BTC0831合約價格為7010美元，現貨價格為701美元，貼水5美元。[2018/9/1]

有點繞，但是我們來整理一下思路。就是我有一個知識，我構造出來一個NP問題使得我這個知識就是我這個NP問題的解。但是你可以檢驗的不是這個NP問題或者這個NP問題的解本身，而是在擁有解的一方將解帶入這個原NP問題并轉化后的另一個問題的完備性。因為你知道，倘若這個人沒有解的話這種轉化是不可能完成，當通過一系列消息交互對這個轉換后的問題的完備性進行考驗之后，你就可以相信這個人是有原NP問題的解的。

2. 舉例說明零知識工作原理及特征

下面我們舉例說明零知識證明的工作原理及特征。首先我們要知道的是。在數字貨幣和區塊鏈中，所有的信息都是數。這個數可以很大，可以有成百上千位。這些數可以被連接成更大的數，也可以被切割成很多稍微小一些的數，用來傳達不同的意義。這些字段可以是錢包地址，可以是金額，可以是交易的簽名，等等。所有的這些信息都是數，很大很大的數。但是本質上跟我們接觸到的正常的數沒有任何差別。 

我也可以把一則消息數字化，比如我可以把一段英文字符完全轉換成很大很大的一個數，這個數就是我們NP問題的解。

我們上面說的三色和四色問題雖然說也是NP問題，但是他們不適用于我們想要實現零知識證明的NP問題。是因為我們很難將解帶入三色和四色問題并且把這個NP問題轉換到另外一個維度上。我們想要的問題是那種可以直接用等式表達其正確性的。這樣的問題比如說求解高維度下的多項式，這個多項式可以是成百上千次方，甚至是百萬次方級別的多項式。求解這樣一個百萬次方的多項式或者說方程，是很困難的。但是我們很容易去驗證一個解。比如說一個數是不是這個一元n次方程的解，我們只需要把這個解代入到原方程當中看它等式兩邊是不是相等就可以了。我們接下來用一個例子來講為什么求解一元N次方程是一個好的NP原問題，那我們也會講到多項式方程把解代入其中之后如何轉換成另一個維度下的另一個問題，而且這種轉換后的NP問題如何可以用于被校驗。

金色相對論丨何永：每個領域的AI算法都有可能和區塊鏈結合:在本期金色相對論上，在談到區塊鏈和AI如何融合時，深腦鏈CEO何永表示，兩個大邏輯:是用區塊鏈解決AI行業問題，還是用AI解決區塊鏈行業問題，第一個邏輯，從AI三要素為切入點，算力、算法、數據，從算力角度區塊鏈可以讓計算節點分布式管理，從而形成分布式AI算力，從算法角度:這個結合點就非常多了，每個領域的AI算法都有可能和區塊鏈結合，從數據角度:區塊鏈可以幫助產生數據、保護數據隱私。第二個邏輯，目前看來結合的機會有限。[2018/7/17]

再次想要重申的是，在區塊鏈和數字貨幣的世界里，所有的信息都是數。和我們平時說的13579、24680，沒有任何區別。在我們的這個例子中為了方便表達，我們用一個比較小的數X=2做例子，這個2就是我們想要證明的知識，就是說我們不想告訴別人我們知道這個數是2，我們也想讓別人相信我知道這個數是2。

現在我們需要構建一個多項式方程而這個多項式方程的解就是2, 我們這里用到的是x^2+2x+1=9。 在實際系統中這個值可以是一個非常非常大的數，有成百上千位。而這個多項式也可以是百萬次方級別的一元N次方程。 

方便的同學可以把這個多項式寫在紙上：x^2+2x+1=9。大家可以看到x=2就是它的解。如果不做任何轉換我除了告訴你這個解好像沒有別的方式讓你相信我。我們需要完成一種轉化，達到我不告訴你解等于2，也能證明我知道這個解。實際系統中的多項式很復雜，我們需要借助計算機完成。但是想讓計算機幫我們轉換轉化，我們就需要一用一套簡單的計算邏輯。計算機需要把上面的多項式打開，每個步驟只干一件事，并引入額外的臨時中間變量存中間的結果。所以，我們可以把x的平方轉化為x乘以x， 2x其實就是2乘以x，前兩項的相加我們把這兩項的中間結果分別定義為t1和t2，所以前兩項的相加結果就是t1加t2，我們再把這個結果定義為中間變量t3。 t3再加上1，就是我們最后的輸出結果。具體說來，我們現在應該有四個等式，t1=x*x， t2=2*x， t3=t1+t2，out= t3+1。這個里面的常量包括1和2，因為他們是線性關系我們只保留1，再把x，t1，t2，t3，out全部提取出來變成一個向量。也就是說一個常量1是第1個元素，未知數x是第2個元素，多項式的輸出output是第3個元素，中間變量t1，t2，t3分別是第4，5，6個元素。這樣的話我們就把這樣一個具有6個元素的向量定義成我們這個系統的solution。也就是解。那其實我們對應的解應該是 （1,2,9,4,4,8），也就是說如果我知道x=2, 那么就很容易構建出來這六個元素組成的向量是（1,2,9,4,4,8）。為了方便表述，我們后面把這個向量成為解向量。

金色財經現場報道丨迅雷CEO陳磊：區塊鏈不應放在實驗室里，而應把其放到實際應用中:金色財經記者現場報道，今日，在博鰲亞洲論壇“再談區塊鏈場”中，迅雷CEO陳磊表示：我們最好不要把區塊鏈放在實驗室里，而是把區塊鏈放到實際的應用當中去。當你把技術放到實際應用當中，每天必須面對使用的壓力，就會逼著提升技術。提升不了用戶就罵你，這是最有效的技術進步的方式。[2018/4/10]

現在我們分別要把t1=x*x， t2=2*x， t3=t1+t2，和out= t3+1寫成解向量表達的形式。我們可以用點乘，也就是內積，的形式將需要的元素過濾出來。我們構建一個向量（0,0,0,1,0,0），這里面唯一一個1對應的是t1在解向量中的位置，再構建向量（0,1,0,0,0,0），這里面的1對應的x在解向量中位置，這樣，t1=x*x，就可以寫成一個解向量的向量內積t1，等于包含有解向量的第二個向量內積x，乘以包含有解向量的第三個向量內積x。這部分在后續的文字版中會加上插圖方便聽眾理解。我們用相同的方式，可以把t2=2*x寫成一個包含有解向量的向量內積t2等于兩個包含有解向量的向量內積結果相乘的形式，同理t3=t1+t2可以寫成解向量的一個向量內積t3等于一個解向量的向量內積乘以1，而這個1其實也是一個解向量的向量內積。這個包含解向量的向量內積等式同樣可以用于表達最后一個等式，就是out= t3+1。

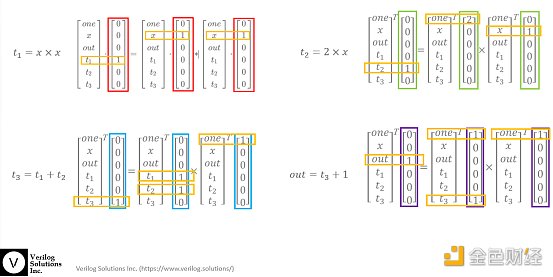
我們發現，我們已經把一個簡單的數字2，變成了一個向量解，而且，這個向量解在經過我們上面的一連串算法變換之后，變成了由四個方程約束的向量解。現在如果我告訴別人這四個約束方程的話，也不能完全達到零知識證明的目的，因為向量解里面包含了我們的真實解x=2。那么怎么辦呢，我們一定要繼續對這四個約束方程在進行變化。

這四個約束方程，其實可以大致寫成C=A x B的形式，這樣的等式有4個。其中每一個中的C，A，B，都對應一個6個元素的常向量，就是我們上面使用的通過內積過濾所需元素的向量。對應于等式左邊，我們把這4個用過內積過濾元素的向量寫成按行排列的矩陣，就得到了一個4行6列的矩陣，對應于等式右邊的A和B，同樣每一個A或者B我們也有4個常向量用于過濾元素，同樣可以寫成一個4行6列的矩陣。所以，我們有三個4行6列的矩陣，分別對應于C，A，和B。為了進一步變換，我們現在將C，A，和B這樣的4行6列的矩陣，按照列向量處理。對應于C的第1列，我們有（0,0,0,0），第二列也是（0,0,0,0），第三列是（0,0,0,1），第四列是（1,0,0,0），第五列是（0,1,0,0），第六列是（0,0,1,0）。同樣對于A和B也是分解成列向量。

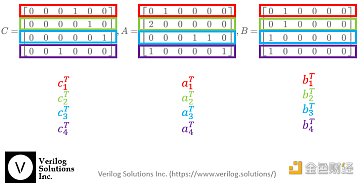
我們用拉格朗日插值法對于每一個這樣的列向量，把每個元素的位置，即n=1,2,3,4作為輸入，得到每一列的解析式。比如，對應于C矩陣的第三列，我們有f(1)=0, f(2)=0, f(3)=0, f(4)=1。使用拉格朗日差值法，我們可以得到第三列的解析式：

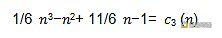
所以我們把C，按列的方向，分別寫成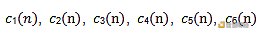6個關于n的三次方解析式。同理A和B矩陣也可以分別寫成6個關于n的三次方解析式。我們把這六個解析式寫成列的形式，即每個矩陣現在被轉化成了一個6x1的列向量，其中每個列向量的每個元素是一個n的三次多項式。此時，我們已經把原問題轉化成了另一個維度的問題。我們用C矩陣對應的列向量的轉置乘以我們的解向量（其結果應該是一個n的三次多項式）應該等于A矩陣對應的列向量的轉置乘以我們的解向量，再乘以B矩陣對應的列向量的轉置乘以我們的解向量，其結果應該是一個n的6次多項式。上面的等式，應該是在n=1, 2, 3, 4時都成立。把右邊挪到左邊變做減法，我們得到了一個三次多項式減六次多項式等于0的形式，并且要求該六次多項式等于0，在n=1,2,3,4時都成立。

要求該六次多項式等于0，在n=1,2,3,4時都成立，其實就是意味著（n?1）（n?2）（n?3）（n?4）是它的子因式，我們把（n?1）（n?2）（n?3）（n?4）定義為Z（n），上面的六次多項式定義為P（n），我們可以求出另外一個子因式，應該是n的2次方多項式，把它定義為H（n）。為了證明我知道原多項式的解向量，此時只需將P（n）與H（n） 發給檢驗者，檢驗者使用Z（n）×H（n） 檢查是否與P（n）相等，即可判斷我是否有正確的解向量。

整個過程中，我們先構建了一個x的二次方程，將x=2擴展成解向量，并用了4個向量方程約束解向量，再把約束方程的參數以矩陣列的形式轉化到另外一個維度成為n的多項式，并用因式分解的形式完成對n的多項式的驗證。可以看到，如果我們不知道解x=2，是無法完成這樣的轉化的。一旦驗證者驗證了這樣的轉化是正確的，那么就可以在不知道x=2的情況向，相信我知道正確的答案。

3. ZKP在區塊鏈中發揮何種優勢

隱私保護是ZKP在區塊鏈中的最大優勢。前面已經提到過，在區塊鏈的世界里，所有的信息都可以表示成數字。類似的，區塊鏈中的狀態轉換也可以用數字的拼接和分割表示不同的意義。說的直白一些，就是區塊鏈的狀態，包括各個錢包地址或者智能合約地址上的狀態轉換，都可以通過編碼數字化。雖然這個數字化的結果是個很大的數，但是也可以構建出一個高階多項式，使得這個數字就是他的解，之后通過我們前面講的方法，構建出零知識證明。這樣，我們可以將區塊鏈上的交易信息隱藏起來，達到隱私保護的目的。

更進一步，我們可以把一連串的交易打包，只記錄這一連串的交易對區塊鏈造成的影響，即增量更新。這種增量更新也可以數字化成一組編碼。那么用同樣的方式，可以達到將一連串交易打包成零知識證明。這也就是zkrollup的最基本的原理了。

4. 分析零知識證明在未來有何前景

正如上面講到的那樣，使用零知識證明，不僅可以隱藏信息增加現有區塊鏈上交易的私密性，同時可以將交易打包增加吞吐量。所以，使用零知識證明相關的技術，將毫無引文催生新的生態和在其上發展的應用。這對DeFi、GameFi、以及未來的元宇宙都具有很實際的意義。比如，一個人和智能合約交互的地址將是不可見的，或者一些交易記錄可以被隱藏。但是我還是可以相信當前的區塊鏈狀態是正確的，是可以被驗證為真實和正確的。同時可以預見的是，對于黑客來講，最終他們的資金來源和流向將變的更加困難。可也會增加項目方和廣大用戶對區塊鏈安全團隊的需求和對智能合約安全性提出更高的要求。

Tags：區塊鏈BSPNBS比特幣區塊鏈個人怎么買BSP幣NBS幣比特幣未來能達到1000萬美金嗎

中幣交易所